はじめに
機械学習をやる上では「勾配降下法」を理解しておきたい。
「勾配降下法」で検索すると自分が書いた記事が見つかります。
yaju3d.hatenablog.jp
資料を元に書いた記事なので当時はよく理解していたわけではないですが、今、読み返すとふむふむと言ったところです。今回はもっと深く追求していきます。
機械学習は最適解を求めるのが目的です。
上記記事の八百屋の件でも、条件が当てはまる最小の値をひたすら繰り返し計算すれば求めることが出来るのですが、これを出来るだけ少ない計算で最小値を見つけるようにしたい。ここで「勾配降下法」を使うことになるわけです。
解けない連立方程式
どうせなので八百屋の問題を使います。
例題 1
リンゴ1個とミカン3個を買うと190円、リンゴ3個とミカン1個を買うと330円するようです。
リンゴ2個とミカン4個を買うといくらになるでしょうか?
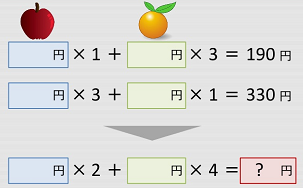
今回は数式で表してみます。次の連立方程式となります。
加減法で計算します。
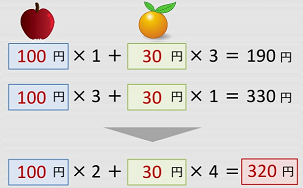

例題 2
例題 1 に対し、更にリンゴ5個とミカン7個を買うと660円を追加した場合
リンゴ2個とミカン4個を買うといくらになるでしょうか?
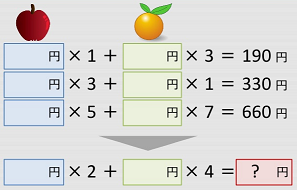
先程と同様に連立方程式を書いてみます。
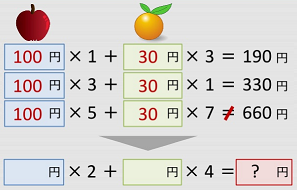
中学校で勉強する連立方程式は、未知数(パラメータの数)が2個であれば、方程式の数も2本でなければなりません。例題 2は、方程式の数が多すぎるということになります。
とは言え、実際の世の中の現象は、このようにデータがバラバラなケースのほうが多いですよね。
そこで出来るだけ近い値である近似値を求めることにするわけです。
近似値を求める
今回、近似値を求めるのには最小2乗法を使います。
下図に合わせて、最小二乗法の式を変更してみます。
最後に平均しているので3で割っていますが、最小値を求める上で平均ではなく合計したままでも、最小二乗法の公式通りに2で割っても最終的に求まる結果は変わらないです。

条件が当てはまる最小の値をひたすら繰り返し計算する。
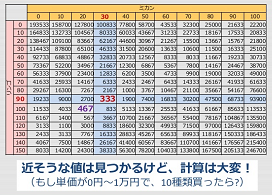
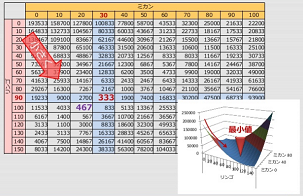

少ない計算で最小値を求める
最小二乗法では1回の計算で(一発で)パラメータを求める方式です。データを追加する度に再度計算し直すことになります。少ないデータ量の時はいいですが、データ量が膨大になるとシステムの対応が難しくなってきます。
もし、データを追加するたびにパラメータを更新していく方式ができるなら、変化点だけの少ない計算で最小値を求めることができるようになります。

それが、「勾配降下法」という方法となります。
続きは後日書きます。