はじめに
予測モデルを推測する分かりやすいサンプルを見つけたので、この資料を基に理解していく。
機会学習勉強会 (2016.2.27)のつぶやき
- 実績データからパラメータを推定。パラメータを使って、結果を予測
- パラメータ特定できない場合、合計金額の誤差が小さくなるような単価を採用する
- 全ての組み合わせを検証するのではなく、少ない計算で最短距離で行う
- 学習:予測式、誤差の計算、誤差の最小とする組み合わせ
- 先程の例を線形回帰(線形重回帰)の式にする
- 誤差を決める。誤差関数と最適化手法を記述
- 学習率が大きすぎても失敗する。
勾配降下法とは
誤差の最小値を求める手法。
パラメータの特定できない場合、誤差が小さくなるような値を採用する。
イメージ例

例題1
たかしくんは八百屋へお使いに行きました。
リンゴ1個とミカン3個を買うと190円,リンゴ3個とミカン1個を買うと330円するようです。
リンゴ2個とミカン4個を買うといくらになるでしょうか?
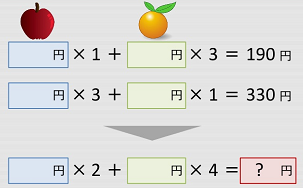

このくらいの問題なら、暗算で求めることが出来ます。
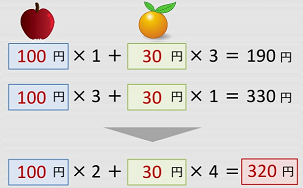

では、次はどうでしょうか?
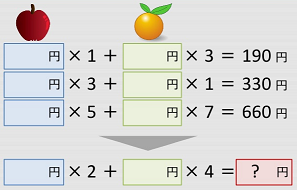
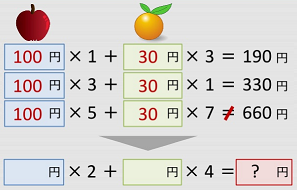

条件が当てはまる最小の値をひたすら繰り返し計算する。
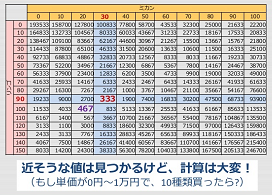
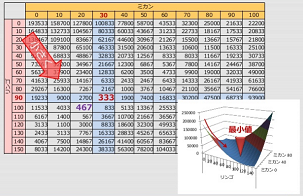
少ない計算で最小値を見つけたい。


TensorFlowで同じように書いていく

TensorFlow のほか高速な配列演算パッケージであるNumPyやプロットしたい場合はmatplotlib.pyplotなど使用するライブラリをロードする。
# 必要なモジュールを読み込む import numpy as np import tensorflow as tf
予測式(モデル)を記述
# 1. 予測式(モデル)を記述する # 入力変数と出力変数のプレースホルダを生成 x = tf.placeholder(tf.float32, shape=(None, 2), name="x") y_ = tf.placeholder(tf.float32, shape=(None, 1), name="y") # モデルパラメータ a = tf.Variable(tf.zeros((2, 1)), name="a") # モデル式 y = tf.matmul(x, a)
- 値を入れる"箱"を作成
入出力 → placeholder,パラメータ → Variable
(注意)shape = (訓練データの数, 次元数)
※"訓練データの数"は None にすると可変長扱い
補足説明
プレースホルダ(placeholder)とは、実際の内容を後から挿入するために仮に確保した場所のこと
tf.placeholderでセットした変数 x や y_ は特定の値ではなくplaceholderと呼ばれ
TensorFlowに計算を実行しろと頼むときに入力する値です。
tf.zerosは、要素が全て「0」である0行列をセット 参照:TensorflowのAPIについて
shape=(行, 列)は、各次元の要素数 (行数, 列数)。
shape=(None, 2)は、2列で後でサイズが決まるような場合に使用する。

shape=(None, 1)は、1列で後でサイズが決まるような場合に使用する。

tf.matmulは行列の掛け算(ここでは定義で実際に使うのは、loss = tf.reduce_mean(tf.square(y_ - y)) )
行列式を使った連立方程式の解き方
ke!san 連立方程式
- 予測式(モデル)を記述

.誤差関数と最適化手法を記述
# 2. 学習に必要な関数を定義する # 誤差関数(loss) loss = tf.reduce_mean(tf.square(y_ - y)) # 最適化手段を選ぶ(最急降下法) train_step = tf.train.GradientDescentOptimizer(0.02).minimize(loss)
mean も average も「平均値」ですが、mean のほうが学術用語で、average のほうが普通語です。
参照:meanとaverageの違いは?
- 誤差関数を記述
ふつうの回帰問題 → 平均二乗誤差
- 最適化手法を選ぶ
・入門 → 最急降下法(勾配降下法) GradientDescent~
※どれを選ぶかで学習(最適化)の速さが変わる
・引数に適度な"学習率"を指定する
※大きすぎると学習失敗(発散)、小さすぎると学習が遅い
訓練データを作成(or読込)
# 3. 実際に学習処理を実行する # (1) 訓練データを生成する train_x = np.array([[1., 3.], [3., 1.], [5., 7.]]) train_y = np.array([190., 330., 660.]).reshape(3, 1) print("x=", train_x) print("y=", train_y)

※予測式で定義した形状(shape)に合わせること
※実用場面では,外部データを(ファイルやSQLなどから) 読みとって2次元配列に整形する。
# (2) セッションを準備し,変数を初期化 sess = tf.Session() init = tf.initialize_all_variables() sess.run(init) # (3) 最急勾配法でパラメータ更新 (100回更新する) for i in range(100): _, l, a_ = sess.run([train_step, loss, a], feed_dict={x: train_x, y_: train_y}) if (i + 1) % 10 == 0: print("step=%3d, a1=%6.2f, a2=%6.2f, loss=%.2f" % (i + 1, a_[0], a_[1], l)) # (4) 学習結果を出力 est_a = sess.run(a, feed_dict={x: train_x, y_: train_y}) print("Estimated: a1=%6.2f, a2=%6.2f" % (est_a[0], est_a[1]))
sess.run ( [出力, ...], feed_dict={入力リスト} )
sess.run を呼び出すことで、"出力"に指定した データフローグラフが計算される
※学習を回すには、先ほど作成した最適化手段(train_step)を出力値に指定して sess.run を呼び出す。
参考: 実行結果


# 4. 新しいデータに対して予測する # (1) 新しいデータを用意 new_x = np.array([2., 4.]).reshape(1, 2) # (2) 学習結果をつかって,予測実施 new_y = sess.run(y, feed_dict={x: new_x}) print(new_y)
予測でも sess.run を用いる
feed_dictには新しい入力値を指定することに留意。(当然ですが...)

最終ソースコード
# coding: utf-8 # 必要なモジュールを読み込む import numpy as np import tensorflow as tf # 1. 予測式(モデル)を記述する # 入力変数と出力変数のプレースホルダを生成 x = tf.placeholder(tf.float32, shape=(None, 2), name="x") y_ = tf.placeholder(tf.float32, shape=(None, 1), name="y") # モデルパラメータ a = tf.Variable(tf.zeros((2, 1)), name="a") # モデル式 y = tf.matmul(x, a) # 2. 学習に必要な関数を定義する # 誤差関数(loss) loss = tf.reduce_mean(tf.square(y_ - y)) # 最適化手段を選ぶ(最急降下法) train_step = tf.train.GradientDescentOptimizer(0.02).minimize(loss) # 3. 実際に学習処理を実行する # (1) 訓練データを生成する train_x = np.array([[1., 3.], [3., 1.], [5., 7.]]) train_y = np.array([190., 330., 660.]).reshape(3, 1) print("x=", train_x) print("y=", train_y) # (2) セッションを準備し,変数を初期化 sess = tf.Session() init = tf.initialize_all_variables() sess.run(init) # (3) 最急勾配法でパラメータ更新 (100回更新する) for i in range(100): _, l, a_ = sess.run([train_step, loss, a], feed_dict={x: train_x, y_: train_y}) if (i + 1) % 10 == 0: print("step=%3d, a1=%6.2f, a2=%6.2f, loss=%.2f" % (i + 1, a_[0], a_[1], l)) # (4) 学習結果を出力 est_a = sess.run(a, feed_dict={x: train_x, y_: train_y}) print("Estimated: a1=%6.2f, a2=%6.2f" % (est_a[0], est_a[1])) # 4. 新しいデータに対して予測する # (1) 新しいデータを用意 new_x = np.array([2., 4.]).reshape(1, 2) # (2) 学習結果をつかって,予測実施 new_y = sess.run(y, feed_dict={x: new_x}) print(new_y) # 5. 後片付け # セッションを閉じる sess.close()
実行結果
リンゴ 98.81 ≒ 99、ミカン 24.90 ≒ 25 → 99 x 2 + 25 x 4 ≒ 297
x= [[ 1. 3.] [ 3. 1.] [ 5. 7.]] y= [[ 190.] [ 330.] [ 660.]] step= 10, a1= 70.35, a2= 46.23, loss=2189.06 step= 20, a1= 83.06, a2= 36.70, loss=771.90 step= 30, a1= 90.13, a2= 31.41, loss=334.34 step= 40, a1= 94.05, a2= 28.47, loss=199.24 step= 50, a1= 96.23, a2= 26.84, loss=157.52 step= 60, a1= 97.44, a2= 25.93, loss=144.64 step= 70, a1= 98.12, a2= 25.42, loss=140.67 step= 80, a1= 98.49, a2= 25.14, loss=139.44 step= 90, a1= 98.70, a2= 24.99, loss=139.06 step=100, a1= 98.81, a2= 24.90, loss=138.94 Estimated: a1= 98.81, a2= 24.90 [[ 297.22738647]]