DLTアルゴリズムでは、点数の2倍の行を持つ下記の行列式に展開します。
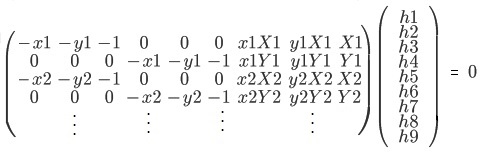
これを特異値分解(Singular Value Decomposition:SVD)を用いて最小二乗法によりを求めます。
下記ソースリストは、コンピュータビジョンの本に記載されているhomography.pyの一部です。
点数の2倍の行列式を生成し特異値分解してを求めていますね。
# 線形法のための行列を作る。対応ごとに2つの行になる。 nbr_correspondences = fp.shape[1] A = zeros((2*nbr_correspondences,9)) for i in range(nbr_correspondences): A[2*i] = [-fp[0][i],-fp[1][i],-1,0,0,0, tp[0][i]*fp[0][i],tp[0][i]*fp[1][i],tp[0][i]] A[2*i+1] = [0,0,0,-fp[0][i],-fp[1][i],-1, tp[1][i]*fp[0][i],tp[1][i]*fp[1][i],tp[1][i]] U,S,V = linalg.svd(A) # 特異値分解 H = V[8].reshape((3,3)) # ホモグラフィパラメータ
※homography.pyでは、更に点群を平均値が0、標準偏差が1になるように正規化していますが、今回はそこまで説明はしません。
では、特異値分解とは何か?
中学の時に因数分解を習ったと思います。覚えてますか?
数学の世界では数理的なモデル(数式)を見通しを良くするために「分解」します。
特異値分解は、「行列」の世界における「分解」なのです。
参照:文系のための「特異値分解」(1)、文系のための「特異値分解」(2)
ちなみに「行列」の世界では割り算は定義されていません、行列に逆数を掛けて割り算と同様な結果を求めるのです。行列に逆数を掛ける際に使用するのが「逆行列」となります。
参照:逆行列を理解してみる
ある行列を特異値分解すると次のように分解されます。
は、「左特異ベクトル」と呼ばれる行列
は、「特異値行列」と呼ばれる対角行列
は、「右特異ベクトル」と呼ばれる行列
U,S,V = linalg.svd(A) # 特異値分解 H = V[8].reshape((3,3)) # ホモグラフィパラメータ
最小二乗法の解は、特異値分解した行列の最後の行に求まっています。その為、V[8]としているのです。
では、実際に射影変換パラメーターの値を求めてみます。
射影変換前の4点座標([0, 0],[160, 0],[160,120],[0,120])
射影変換後の4点座標([20, 20],[140, 0],[160,120],[0,120])

ホモグラフィの取得メソッド(homography.H_from_points)を使う上で、左上から反時計回りに([[Y1,Y2,Y3,Y4],[X1,X2,X3,X4],[1,1,1,1]])と値を指定します。
※座標指定が(Y,X)の順なのは、行列の行成分がY座標で列成分がX座標となり行→列の順で表すからでしょうかね。
fp = array([[0,120,120,0],[0,0,160,160],[1,1,1,1]]) tp = array([[20,120,120,0],[20,0,160,140],[1,1,1,1]]) H = homography.H_from_points(fp,tp)
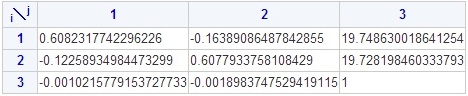
パラメータ結果 指数表示→小数第4位で書式変換
6.04166667e-01, -1.25000000e-01, 2.00000000e+01 → 0.6041, -0.1250, 20.0000 -1.66666667e-01, 6.04166667e-01, 2.00000000e+01 → -0.1666, -0.6041, 20.0000 -1.90972222e-03, -1.04166667e-03, 1.00000000e+00 → -0.0019, -0.0014, 1.0000
下記は以前の記事で8次元連立方程式で求めた際のパラメータ結果です。ほぼ近似値ですよね。
■ 特異値分解の他の利用方法について
特異値分解で分解を行うことで、「擬逆行列」と「固有値」を求めるのが非常に楽になります。
「擬逆行列」は、擬似的に求めた逆行列のことです。逆行列は、正方行列(行数と列数が一致 例 4行x4列)の場合のみ求めることが出来ます。
今回のようにDLTアルゴリズムでは点数によって行数が可変し、4点なら8行x9列の行列となり正方行列になりません。よって擬逆行列を使うことになり、擬逆行列は「特異値分解」から導くことが出来ます。
参照:文系のための「擬逆行列」
「固有値」は、「固有値ってなに?」で「個々のデータの主成分方向の情報量の総和から算出した標準偏差の2乗のこと」と説明しています。
「固有値と固有ベクトル」はセットで使われ、主成分分析ではもっとも大きい固有値に対応する固有ベクトルのことを、第1主成分と呼び、n番目に大きい固有値に対応する固有ベクトルを第n主成分と呼ぶ。
「行列の固有値って何だろうか」の資料では、固有値の性質を下記の2点としている。