逆行列を理解してみる - デジタル・デザイン・ラボラトリーな日々

画像の変形処理を行う上で逆行列を行う処理があり、理解がとぼしいためか頭が混乱してきます。
以前、テクスチャの仕組みを理解しようとした際にも、逆行列が出てきました。

あらためて、逆行列とはなんなのかをイチから理解していこうと思います。

行列には、足し算・引き算・掛け算は定義されているのですが、割り算は定義されていません。
では、行列で割り算が出来ないかというとそうではありません。

行列ではなく自然数の場合、「1」に「3」を掛けると「3」となります。これを元の「1」に戻す場合、「3で割る」ことで元の「1」になりますが、「1/3を掛ける」としても元の「1」になります。
この場合、「3で割る」とは言わずに「1/3を掛ける」と考えます。
割り算のかわりに逆数を掛けることで、割り算と同様の結果が求めることが出来るのです。

行列でも同じ様に「逆数を掛ける」に近い考え方をします。
行列に逆数を掛ける際に使用するのが、「逆行列」となるのです。

「逆行列」の例を示す前に「単位元」について説明します。
単位元とは、演算をしても何も変わらないような要素のことです。
整数で「乗法」という演算を考えたとき、「1」が単位元であり、「加法」では「0」が単位元となります。数学としては、記号「E」(ドイツ語の「1」を表す「etin」の頭文字)で表されます。
行列における単位元は「単位行列」と呼び、2x2行列の場合は下記となります。
$E=\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$
このように、右下がりの対角線上にある成分がすべて「1」で、残りの成分がすべて「0」となります。

逆行列の例を示します。
逆行列には、下記の公式(2x2行列)があります。他の3x3行列と4x4行列の逆行列は「逆行列」サイトを見てください。
$A=\begin{pmatrix} a & b \\ c & d \end{pmatrix}$
についてdetA=ad-bc≠0のときAの逆行列が存在して
$A^{-1}=\displaystyle{\frac{1}{ad-bc}\begin{pmatrix} d & {-b} \\ {-c} & a \end{pmatrix}}$ 　

例えば、 $\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}$ 　の逆行列は　 $\displaystyle{\frac{1}{-2}\begin{pmatrix} 4 & {-2} \\ {-3} & 1 \end{pmatrix}}$ 　となります。

分母は、 $ad-bc = 1\times4-2\times3=4-6=-2$ で求まります。

上述で3に1/3を掛けると1(単位元)になると説明しましたね。
それを一般式に表すと下記になります。
$AA^{-1}=E$

行列で展開してみます。※2x2行列の積の公式
$\displaystyle{\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\frac{1}{-2}\begin{pmatrix} 4 & {-2} \\ {-3} & 1 \end{pmatrix}=\frac{1}{-2}\begin{pmatrix} 1\times4 + 2\times{-3} & 1\times{-2} + 2\times1 \\ 3\times4 + 4\times{-3} & 3\times{-2} + 4\times1 \end{pmatrix} =\frac{1}{-2}\begin{pmatrix} {-2} & 0 \\ 0 & {-2}\end{pmatrix}}$

$\displaystyle{\frac{1}{-2}\begin{pmatrix} {-2} & 0 \\ 0 & {-2}\end{pmatrix}=\begin{pmatrix} {1} & 0 \\ 0 & {1}\end{pmatrix}}$

掛け算には交換法則が成り立ちますので、
今度は、左右入れ替えて計算してみます。

$\displaystyle{\frac{1}{-2}\begin{pmatrix} 4 & {-2} \\ {-3} & 1 \end{pmatrix}\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}=\frac{1}{-2}\begin{pmatrix} 4\times1 + {-2}\times3 & 4\times2 + {-2}\times4 \\ {-3}\times1 + 1\times3 & {-3}\times2 + 1\times4 \end{pmatrix} =\frac{1}{-2}\begin{pmatrix} {-2} & 0 \\ 0 & {-2}\end{pmatrix}}$

$\displaystyle{\frac{1}{-2}\begin{pmatrix} {-2} & 0 \\ 0 & {-2}\end{pmatrix}=\begin{pmatrix} {1} & 0 \\ 0 & {1}\end{pmatrix}}$

このように左右どちらから掛けても単位行列の「E」になります。つまり「逆数を掛ける」は、「割る」に相当します。
参考:２Ｘ２行列の逆行列の計算

■逆行列を使用した座標変換
以前の記事「画像の回転処理　穴が空かない方法」では行列を使用してませんでした。
今回、逆行列を使用した場合での説明を書いてみます。

画像を回転させた時に穴が空いてしまう問題があります。
f:id:Yaju3D:20130430230100j:plain

これは転送元から転送先にピクセルを移動した際に、(0.5,0.5)など小数の座標があった場合に小さい方に寄せたりすると起きる問題です。
f:id:Yaju3D:20130430230125j:plain

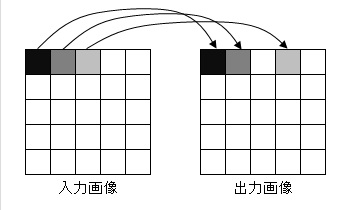
これを解決するには、転送先から転送元にピクセルを移動すればいいのです。
この時に逆行列を使用します。
f:id:Yaju3D:20130430234347j:plain
f:id:Yaju3D:20130430230050j:plain
転送元(src)から転送先(dst)に座標を求める変換行列を $T$ とすると
$\begin{pmatrix} x' \\ y'\end{pmatrix}=\Large T\begin{pmatrix} x \\ y\end{pmatrix}$

変換行列 $T$ を回転行列とすると
$\begin{pmatrix} x' \\ y'\end{pmatrix}=\begin{pmatrix} cos & {-sin}\\ sin & cos\end{pmatrix}\begin{pmatrix} x \\ y\end{pmatrix}$

これを転送先(dst)から転送元(src)の座標を求めるのに使用するのが逆行列です。
$\begin{pmatrix} x \\ y\end{pmatrix}=\Large T^{-1}\begin{pmatrix} x' \\ y'\end{pmatrix}$

$\Large T^{-1}=\frac{1}{cos^2+sin^2}\begin{pmatrix} cos & sin \\ {-sin} & cos\end{pmatrix}$

分母の $cos^2+sin^2$ は、ピタゴラスの定理で「1」となるので
$\Large T^{-1}=\begin{pmatrix} cos & sin \\ {-sin} & cos\end{pmatrix}$
これは回転角が「−θ」となった逆回転となります。参照:回転行列

$\begin{pmatrix} x' \\ y'\end{pmatrix}=\begin{pmatrix} cos & sin\\ {-sin} & cos\end{pmatrix}\begin{pmatrix} x \\ y\end{pmatrix}$

※今回説明上は2x2行列にしましたが、一般的には平行移動も加えた3x3行列が使われます。

もう1つの逆行列を使用した座標変換として、以前の記事「テクスチャマッピングを理解してみる」では、貼り付け先のテクスチャの座標を求める際に、逆行列を使用しました。

テクスチャマッピングでは、ポリゴンとして三角形を利用します。三角形では2辺が求まれば残りは1辺は自動的に決まるので便利です。

貼り付け元のテクスチャ上でのベクトルを A および B 、描画先でのベクトルを A' および B' とします。
f:id:Yaju3D:20130713232917j:plain

テクスチャマッピングの画像を変形する前に、三角形の2辺である現在位置(Ax,Ay)または(Bx,By)と移動先(A'x,A'y)または(B'x,B'y)は既に求まっている状態なので、後は描画結果を変形するための、transformメソッドの引数で使う変換マトリックス(a,b,c,d)を求めることになります。

ベクトルAとBのアフィン変換を連立方程式にすると下記となります。
$A'x = a\times Ax + c\times Ay$
$A'y = b\times Ax + d\times Ay$
$B'x = a\times Bx + c\times By$
$B'y = b\times Bx + d\times By$
さらに行列に変換します。
$\begin{pmatrix} A'x \\ B'x \end{pmatrix}= \begin{pmatrix} a\\ c\end{pmatrix}\begin{pmatrix} Ax & Bx \\ Ay & By \end{pmatrix}$

$\begin{pmatrix} A'y \\ B'y \end{pmatrix}= \begin{pmatrix} b\\ d \end{pmatrix}\begin{pmatrix} Ax & Bx \\ Ay & By\end{pmatrix}$

a,cを求めるので式を変形します。
$\displaystyle{\begin{pmatrix} a \\ c \end{pmatrix}=\frac{ \begin{pmatrix} A'x\\ B'x\end{pmatrix}}{\begin{pmatrix} Ax & Bx \\ Ay & By \end{pmatrix}}}$
行列には割り算の定義は無いので、分母を逆行列に変換します。
$\displaystyle{\begin{pmatrix} Ax & Bx \\ Ay & By\end{pmatrix}^{-1}= \frac{1}{AxBy-BxAy}\begin{pmatrix} By & {-Bx} \\ {-Ay} & Ax \end{pmatrix}}$

逆行列を使用した掛け算にします。

$\displaystyle{\begin{pmatrix} a \\ c \end{pmatrix}= \begin{pmatrix} A'x\\ B'x\end{pmatrix}\frac{1}{AxBy-BxAy}\begin{pmatrix} By & {-Bx} \\ {-Ay} & Ax \end{pmatrix}}$

b,dも同様の式に変換します。
$\displaystyle{\begin{pmatrix} b \\ d \end{pmatrix}= \begin{pmatrix} A'y\\ B'y\end{pmatrix}\frac{1}{AxBy-BxAy}\begin{pmatrix} By & {-Bx} \\ {-Ay} & Ax \end{pmatrix}}$

求めたパラメータをtransformメソッドにセットすると平行四辺形に画像が変換されます。
※ここでは平行移動は無視しています。
g.transform(a, b, c, d, 0, 0);
g.drawImage(img, 0, 0);