はじめに
機械学習の学習すると必ず出てくる用語にシグモイド関数があります。
今回はこれを理解してみたいです。
シグモイド曲線
シグモイド曲線は入力した値を0から1の間に収めてくれる関数の1つです。
多くの自然界に存在する事柄は、このようなS字曲線を取ります。
欠点として1に近づくほど1そのものにならない性質があります。
使う理由
分類した場合に「1」と「-1」という2択ではなく、シグモイド関数は確率で分類すると考えます。
Aの確率が80%で、Bの確率が20%といった感じで分類していきます。
シグモイド曲線の値は 0 から 1 の間になるので確率として使用できます。
すべての関数は微分ができるわけではありません。
尖った点があったり、線が切れていると微分はできないのです。
※尖っていた場合、同じ点に対して二つの傾きが計算できてしまうので微分不可能になる。
どうしてシグモイド関数は滑らかな関数なのか - Qiita
自然科学のための数学2014年度第10講
例えば有名な例として絶対値の関数 があります。この関数は
で微分できません。
同様にステップ関数も で微分できません。

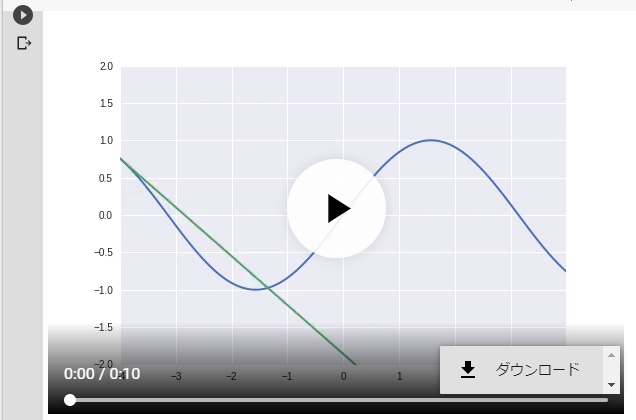
シグモイド関数は下図グラフで示すようにステップ関数を滑らかにした形で線が切れてないので微分が可能になるのです。
数式
グラフ

下図に示すステップ関数(step function)を滑らかにしたものであると見なすことができる。

シグモイド関数の性質
いいサイトがあった。 risalc.info
単調増加性
数学での単調とは「上がったり下がったりがない」という意味です。
放物線は、単調減少と単調増加があります。

シグモイド関数は、S字を描きますが徐々に上がり続けて下がりませんよね。
シグモイド関数の微分
前提
結論
とした時、
導出
逆数の微分
まず、逆数の微分公式を確認しておきます。
です。
逆数の微分公式の証明:「 商の微分公式の証明と例題」
商の微分
シグモイド関数は の逆数なので
ここで、
であるから、式を当てはめると
もう少し詳しい説明を書いてみました。
yaju3d.hatenablog.jp
グラフ
左図はシグモイド関数の微分したグラフ、右図は正規分布関数のグラフです。形が似ていますよね。
正規分布関数との類似性と計算のしやすさの2つが、機械学習でシグモイド関数がよく使われる理由なのです。

使い道
シグモイド関数の微分( )はどこに使われるのか、最急降下法(勾配降下法)や 誤差逆伝播法(バックプロパゲーション)にてパラメーターの更新に使われます。
以前はシグモイド関数が主流でしたが、最近ではReLU関数などが使われています。これは勾配消失の問題です。
シグモイド関数の微分の最大値はとなるため、ディープラーニングで層を増やしていくと勾配が消失してしまうのです。その点、ReLU関数の場合は最大値が
で勾配消失がしにくくなる。
- ニューラルネットワークの基礎を初心者向けに解説してみる | ロボット・IT雑食日記
- 誤差逆伝播法を宇宙一わかりやすく解説してみる | ロボット・IT雑食日記
- 誤差逆伝播法(backpropagation:バックプロパゲーション)とは~制御工学の基礎あれこれ~
- Pythonでニューラルネットワーク - 元理系院生の新入社員がPythonとJavaで色々頑張るブログ
- 活性化関数についてのまとめ(ステップ関数・シグモイド・ReLU等々) | pekochin
ロジスティック回帰との関係
ロジスティック回帰は、以下の数式で表現できます。
シグモイド関数と同じ形であり、数式の中の「」という部分は重回帰分析と同じです。
よって、ロジスティック回帰のグラフを描くとシグモイド関数と同様になります。
ロジスティック回帰の最尤関数
統計学や機械学習をを勉強していると「尤度(ゆうど)」という概念に出会います。
尤もらしい(もっともらしい)ということで、最尤度は最高にもっともらしいってことですね。
尤度とはある事象が観測された時、それぞれの事象の確率の確率分布関数のパラメータがどれだけ尤もらしいかを測る量で、事象の同時確率として定義されます。
※同時確率とは、サイコロを2回投げた場合、1回目に1の目が出て、2回目に2が出る確率は?って聞かれたら、まずで1が出て、次に
で2が出て、それが続けて起こる確率は掛け算を使って、
回帰の時の2乗誤差だった場合は最小化した値を求めるのが目的だったのに対し、今考えるのは同時確率で確率が高くなって欲しいので最大化するのが目的になります。
上記のロジスティック回帰をシグマに展開すると下記式になります。
同時確率を一般式すると下記式になります。
掛け算というのは計算が大変なので、掛け算を足し算にする「対数」を使って尤度関数を表すと下記式になります。
活性化関数として
人間の脳は神経細胞(ニューロン)のネットワークで構成されています。この最小単位の神経細胞(ニューロン)を模倣したモデルがパーセプトロンとなります。このモデルは入力値が閾値を超えた場合に「1」を出力(この場合を「ニューロンが発火する」と表現)し、そうでない場合は「0」を出力します。このように入力値から出力値を生むまでの計算を活性化関数と呼びます。
パーセプトロンでは活性化関数に下図のステップ関数(入力に対してある閾値を境に階段(ステップ)のように出力が1か0か決まる)を使っていました。

ニューラルネットワークは学習をする際に微分を含む計算を行うため、微分するとゼロになるステップ関数は都合が悪いことからステップ関数に似た形で微分してもゼロにならないシグモイド曲線(sigmoid)などが使用されるようになりました。
※微分するとゼロになると都合が悪いのは、値を微分値で更新しても同じ値のままになってしまうからです。
下図のExcelで、106行目の重みの値を更新する際に、前行(105行目)の重みと同行の赤枠「学習係数 x 勾配」の値を加算した値にします。
もし、勾配の値がゼロになってしまうと次の重みの値が更新されないため同じ値のままになり都合が悪くなります。
つまり、そこが正解値ならいいのですが、まだ途中段階で更新が止まってしまうのが良くないわけです。

最後に
今回、シグモイド関数とロジスティック回帰の関係が分かりました。
自分がまだ微分の知識が足りてないってことが分かりました、数式はまだまだ苦手だな。