3Dを基礎から勉強する　正規化 - デジタル・デザイン・ラボラトリーな日々

ベクトルの正規化とは、ベクトルの方向は維持しつつ大きさを「1」にする事を指します。
この大きさが「1」のベクトルのことを単位ベクトルと呼びます。
f:id:Yaju3D:20130608155150j:plain

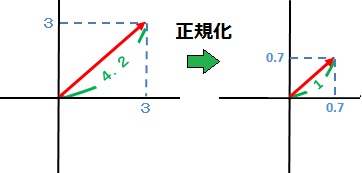
左図の座標(3,3)にあるベクトルの大きさは、 $\sqrt{x^2+y^2} =\sqrt{3^2+3^2}=\sqrt{9+9}=\sqrt{18}=4.2426$

数学者は、2本の垂直な線を両脇に置くことでベクトルの大きさを表します。
ベクトルの大きさ　 $|v|$

ベクトルを正規化する際には、ベクトルの各成分をベクトルの大きさで除算します。
数式は下記となります。Nは正規化の英語(normalize)です。
$N=\frac{v}{|v|}$

右図を正規化した場合、ベクトルの大きさを「1」とするので、各成分は0.7となります。
$N=\frac{3}{|4.2462|}=0.7065$

単位ベクトルを作っておけば、定数倍して簡単にいろんな大きさのベクトルが作れるようになります。
f:id:Yaju3D:20130608193254j:plain

※補足
数学的なお話として、「7cmで35gの棒は、15cmで何gになりますか」という問題があった場合、下記の比例式となります。
7:35 = 15:x
これは、7cmが35(g)だから1cmでは35(g)÷7となり、15cmでは35(g)÷7×15 = 75(g)となります。
このように1cmあたりの重さにしてから15cm分の長さを求めるという考え方を「帰一法」と呼びます。正規化するのもこの考え方と同じになります。

3次元のベクトルの正規化プログラム

    // 長さ
    Point3D.prototype.length = function () {
        return Math.sqrt(this.x * this.x + this.y * this.y + this.z * this.z);
    };

    // 正規化
    Point3D.prototype.normalize = function (thickness) {
        var l = this.length();
        if(l) {
            this.scale(thickness / l);
        } else {
            this.z = thickness;
        }
    };

    // 比率
    Point3D.prototype.scale = function (s) {
        this.x *= s;
        this.y *= s;
        this.z *= s;
    };

■正射影(内積)
内積の便利な性質のひとつに、あるベクトルをもう一つのベクトルに投影(射影)することができます、投影とは影のことです。
下図にて光源をベクトル $\mid A \mid$ の真上からベクトル $\mid B \mid$ を照らしている場合、投影の長さはベクトル $\mid B \mid$ で定まる直線上にできるベクトル $\mid A \mid$ の影の長さになります。この長さを $\mid A \mid$ の正射影(垂直に光を当てたときに出来る影)といいます。

正射影を求めるには投影される側のベクトル $\mid B \mid$ を正規化する必要があります。
何故、正規化するのか見てみましょう。

内積の定義 $\vec{a} \cdot \vec{b} = \mid \vec{a} \mid \mid \vec{b} \mid cos\theta$

図に合わせて式の表現を変更します。
$A \cdot B = \mid A \mid \mid B \mid cos\theta$
$\mid B \mid$ を正規化した結果、 $\mid A \mid cos\theta$ となります。　
f:id:Yaju3D:20130608220903j:plain

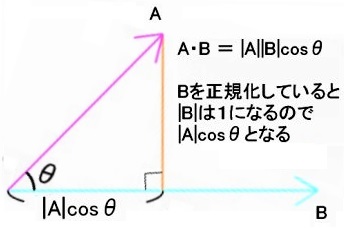
cosθは直角三角形の「底辺/斜辺」であり、斜辺の長さが $\mid A \mid$ とすると底辺 = $\mid A \mid cos\theta$ となります。

正規化した内積の値というのは「標準化ベクトル $\mid B \mid$ を含む直線にベクトル $\mid A \mid$ を真っ直ぐ下ろした時の長さ」になることがわかります。これにより底辺が求まるわけです。また、外積と組み合わせると垂直の長さが求めることも出来ます。点と線の距離を求める（２次元３次元）

この投影は何に使うのかといえば、衝突判定を例にとると、ある点の物体1のポリゴンの頂点などから別の物体2のポリゴン面のへの「最短距離」を求める場合に使用します。また斜めの壁にボール衝突させた場合の反射ベクトルを求めるのにも使われます。
応用例として下記サイトの地面の傾斜に合わせてキャラクターを移動させることにもに使えます。
座標にもっとも近い線分上の点を内積で求める

射影ベクトルが重要だと理解できるには、あるベクトルを色々な基底で分解することを考える場合でしょう。図形の問題で情報量を増やすために補助線を引くと三平方の定理が使えて問題が解ける感覚と同じかな。

■面法線(外積)
正規化の使い方で正射影は内積だとすると、面法線が外積となります。

前回、外積の使い方を説明しました。
最後の面法線ベクトル(n)と光源ベクトル(l)の角度により面の明るさが求める際に、外積の正規化を使用します。

実際に面HGFEの明るさを求めてみます。
f:id:Yaju3D:20130609135702j:plain

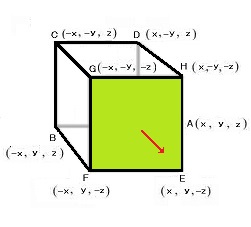
   　  x   y   z
   P1  25 -25 -25  頂点H ( x,-y,-z)
   P2 -25 -25 -25  頂点G (-x,-y,-z)
   P3 -25  25 -25  頂点F (-x, y,-z)
   P4  25  25 -25  頂点E ( x, y,-z)

V1=P2-P1 = (-50,0, 0) 、V2=P4-P1 = (0,50,0)、n = cross(V1,V2) = (0,0,-2500) となります。
外積の大きさは、 $\sqrt{x^2+y^2+z^2} =\sqrt{0^2+0^2+(-2500)^2}=2500$
正規化するので各成分(0,0,-2500)を2500で割ると、(0,0,-1)が求まります。
このz成分がsinθの値となります。
$N=\frac{2500}{|(0,0,-2500)|} = (0,0,-1)$
外積の定義で、両ベクトル $\vec{a}$ と $\vec{b}$ を正規化で「1」にするとsinθが求まることが分かります。
$\vec{a} \times \vec{b} = \mid \vec{a} \mid \mid \vec{b} \mid sin\theta = 1 \times 1 \times sin\theta = sin\theta$

求まった法線ベクトルが(0,0,-1)、光源を(0, 0, -1)とした場合、この内積を計算すると
$\vec{a}=(a_1,a_2,a_3)$ =(0,0,-1) , $\vec{b}=(b_1,b_2,b_3)=(0,0,-1)$
$\vec{a} \cdot \vec{b} = a_1b_1 + a_2b_2 + a_3b_3=0 \times 0 + 0 \times 0 + (-1) \times (-1) = 1$

f:id:Yaju3D:20130526212554j:plain

cosθ=1が0°(垂直)となり最大の明るさになります。

f:id:Yaju3D:20130525230936j:plain

面の明るさの取得プログラム

  // 単位法線ベクトル 外積
  var v1 = p2.subtract(p1);
  var v2 = p4.subtract(p1);
  var n = v1.cross(v2);
  // 正規化
  n.normalize(1);
  // 光源の方向ベクトルとの内積
  var l = new Point3D(0, 0, -1);
  // 面の明るさ
  var product = n.dot(l);

  //productが面の明るさ(cosθ)
  var b = (63 * product + 192) | 0;
  var rgb = 'rgb(' + b + ',' + b + ',' + b + ')'; //min 192 ～ max 255