はじめに
前回の記事の続きとなります。
yaju3d.hatenablog.jp
最終的な更新式を求めたところまでやりました。
パラメータ と
の更新式は、最終的に下記のようになります。
参考
やる夫で学ぶ機械学習 - 多項式回帰と重回帰 - · けんごのお屋敷
多項式回帰
プロットしたデータにフィットさせる際に1次関数の場合は形が直線にしかなりません。
しかし、場合によっては曲線の方がプロットしたデータにフィットする。
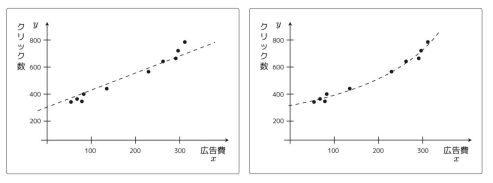
これは関数 を2次関数として定義することで実現できる。
もっと大きな次数にすることも出来る。その場合はより複雑な曲線に対応できるようになる。
しかし、次数を増やせば増やすほどいい感じになるわけではない。確かにフィットするようにはなるけど、過学習と呼ばれる別の問題が発生するようになる。
更新式を求める
前回と同じように を
に偏微分して更新式を求めます。
と
は計算対象外なので除外します。残った
は微分して
になります。
最終的な更新式
最終的なパラメーターの更新式は下記のようになります。
これはパラメーターが、 、
、
と増えていっても同じような更新式になります。
ということは、 番目のパラメーターの更新式は下記のようにできる。
※ となることを利用する。
このように多項式の次数を増やした関数を使うものは、多項式回帰と呼びます。
※誤解されないように説明しておくと、 や
は
乗という意味ではなくて、
番目の学習用データを参照する意味である。
最後に
今回はここまで、次回は重回帰となります。


