ディープラーニング(深層学習)を理解してみる(勾配降下法：ベクトル、内積、微分、偏微分)

はじめに

幾つかの人工知能関連の本やWebサイトを見ても、数式やプログラムのソースリストは記載されていても、数学が苦手な自分が理解できるようになるまでの説明が無い、そんな中でも下記3つの本(Kindle)がまだ理解できそうな感じで参考になりそうである。

計算方法に入る前にベクトル等の基礎知識を先に説明していきます。

ベクトル

ベクトルとは大きさと向きを持つ量と定義されます。
f:id:Yaju3D:20171001213101p:plain

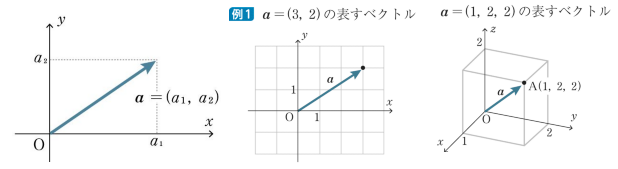
ベクトルの矢を座標平面上に置くことで座標のように表現できます。矢の始点を原点に置き、矢の終点の座標でそのベクトルを表します。これをベクトルの成分表示といいます。
成分表示されたベクトル $a$ で下図のように表現します。また3D座標上でもz軸方向を追加して同じように表現します。
f:id:Yaju3D:20171001225146p:plain

下図のように矢印がたくさんある図を見たことがありませんか?
各データは、どこかの一点のデータを基準にして、大きさと向きを持つベクトルとなります。
f:id:Yaju3D:20171001213359p:plain

内積

ベクトルにも足し算と引き算があるように掛け算も…といいたいところですが、微妙に違うのが内積です。内積だとベクトル同士を掛け算っぽくするのに結果はベクトルではなくスカラという1つの値となります。内積以外にも外積がありますが、ここでは説明しません。

過去に3Dの勉強用に書いた記事がありますので、興味があれば読んでみて見ください。

なぜ内積の計算をそうするのかは次のサイトの説明が分かりやすいと思います。
www.yukisako.xyz

内積というのは2つのベクトルの“近さ”を表しているという程度に理解しておけばいいです。
2つのベクトルの近さを表すのに $cos\theta$ が使われます。

f:id:Yaju3D:20171001231022p:plain

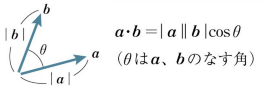
高校までの数学だと「内積の値が $cos\theta$ を使って表される」と教わるが、逆に「 $cos\theta$ の値が内積によって定義されるのだ」と考えるようにするといいでしょう。

$cos\theta$ の値は2つのベクトルの向きが反対なら「-1」、同じであれば「1」となる。 f:id:Yaju3D:20171002005747p:plain

（ア）2つのベクトルが反対向きのときに内積は最小値
（イ）2つのベクトルが平行でないとき、内積は平行の場合の中間の値
（ウ）2つのベクトルが同じ向きのときに内積は最大値

そして、（ア）の内積が最小値というのが、勾配降下法の基本原理となります。

手書き数字認識でどの数字か分類できるのは、より似ているかで判断しています。
方向が似ているベクトルを「似ている」と判断するなら、2つのベクトルが似ていると内積は大きくなるのです。
f:id:Yaju3D:20171002005805p:plain

内積の計算

平面(2次元)
f:id:Yaju3D:20171002005819p:plain

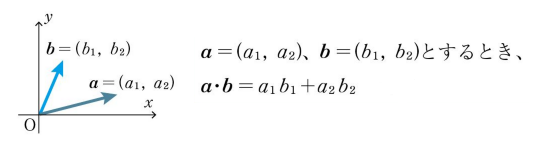
立方空間(3次元)
f:id:Yaju3D:20171002005835p:plain

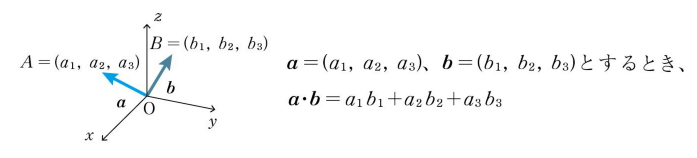
内積は2次元や3次元に限らず、何次元のベクトルについても計算することができます。現実世界では4次元や10次元ベクトルで表せるものは存在しないですが、数学上は計算できるところが数学のおもしろいところでもあります。

この内積が何次元(多次元)であっても計算できるということが重要なポイントです。
リンゴとミカンの値段を求める際は2変数です、それにブドウを付け加えると3変数になり、レモンも付け加えると4変数になります。変数が多くなることを多変数と言います。この多変数というのは機械学習における多次元と同じ意味を持っています。

参照

微分

微分とは、ある関数の各点における傾き(変化の割合)のことです。
そして勾配降下法においては、傾きの最小値を求めることが目的です。 f:id:Yaju3D:20171007211313p:plain

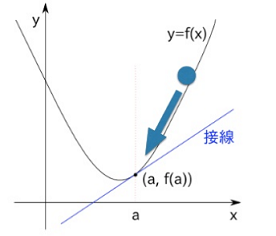
最小値

微分において、傾きが水平になる 0 が最小値といいたいところですが、下図右のように最大値においても水平になり 0 となります。
f:id:Yaju3D:20171008132102p:plain

このことは、勾配降下法においては厄介な性質になります。
f:id:Yaju3D:20170917223314p:plain

導関数

関数 $y=x^{2}$ を微分して得られた導関数は指数を係数にした ${y}'=2x$ となります。
微分の定義式では極限の記号 $\displaystyle \lim_{h \to 0}$ を使って、x の変化量 h を限りなく 0 に近づけます。

$\displaystyle \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}={f}'(x)$

※現代の数学では、0 で割る(分母が0)ことは禁止事項とされているので、極限まで 0 に近づければいいという屁理屈です。

ちなみに、 $'$ の名称は「プライム」で、 $\lim$ の名称は「リミット」と読み、極限(limit)を取る記号です。

https://sci-pursuit.com/math/differential-1.htmlsci-pursuit.com

関数 $y=x^{2}$ は変数が1つでしたが、リンゴとミカンの値段を求める場合は2変数による関数 $z=f(x,y)$ となります。このように変数が2つ以上の関数を多変数関数といいます。
多変数関数でも微分法を適用できます。ただし変数が複数あるので、どの変数について微分するかを明示しなければなりません。この意味で、ある特定の変数について微分することを偏微分(partial derivative)といいます。
例えば、2変数x，yから成り立つ関数を考えてみましょう。変数xだけに着目してyは定数と考える微分を「xについての偏微分」と呼び、次の記号で表します。

$\displaystyle\frac{\partial z}{\partial x}=\frac{\partial f(x,y)}{\partial x}=\lim_{x \to 0}\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}$

yについての偏微分も同様です。

$\displaystyle\frac{\partial z}{\partial y}=\frac{\partial f(x,y)}{\partial y}=\lim_{y \to 0}\frac{f(x,y+\Delta y)-f(x,y)}{\Delta y}$

ちなみに、 $\partial$ の名称は「デル」、 $\Delta$ の名称は「デルタ」です。

関数 $z=x^{2} + y^{2}$ を偏微分すると指数を係数にした $\displaystyle\frac{\partial z}{\partial x}=2x$ 、 $\displaystyle\frac{\partial z}{\partial y}=2y$ となります。

remedics.air-nifty.com

www.youtube.com

勾配降下法に適用

上述で説明してきたベクトルと内積と偏微分が勾配降下法にどのように使われるのか？

勾配降下法は、少しずつ下りながら、場所ごとに最も急な勾配を探すことになります。
$P0$ から最も勾配の急な点 $P1$ の位置を求める。その位置 $P1$ から更に最も勾配の急な点 $P2$ の位置を求める。このように繰り返すことで最も早く最小点にたどり着くようになります。 f:id:Yaju3D:20170924211620p:plain

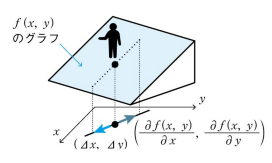
関数 $z=f(x,y)$ において、xをΔxだけ、yをΔyだけ変化させたとき、関数 $z=f(x,y)$ の変化は下記式となります。
$\displaystyle \Delta z = f(x + {\Delta x},y + {\Delta y}) - f(x,y)$
これを近似公式から次の関係が成立します。
$\displaystyle \Delta z = \frac{\partial f(x,y)}{\partial x}{\Delta x} + \frac{\partial f(x,y)}{\partial y}{\Delta y}$

f:id:Yaju3D:20171010235143p:plain

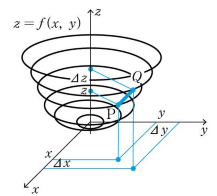
そして、これは2つのベクトルの内積を表す式になっているのです。 f:id:Yaju3D:20171010234406p:plain

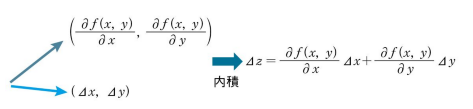
ベクトルが反対向きになっている時に、内積が最小値となっている。 f:id:Yaju3D:20171011001024p:plain f:id:Yaju3D:20171011001230p:plain

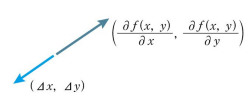
ベクトルが反対向きは、 $-1$ となり、勾配降下法の基本式は次のように表せます。( $\eta$ は正の小さな定数)
$\displaystyle({\Delta x}, {\Delta y})=-\eta\left(\frac{\partial f(x,y)}{\partial x}, \frac{\partial f(x,y)}{\partial y} \right)$

ちなみに、 $\eta$ はイータと読むギリシャ文字です。ローマ字のiに対応します。
なぜループカウンタ変数のほとんどに “i”が使用されるのか？ - Qiita

重要なのは、内積は何次元(何変数)のベクトルについても計算することができます。

$\displaystyle({\Delta x_1}, {\Delta x_2}, \cdots, {\Delta x_n})=-\eta\left(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \cdots, \frac{\partial f}{\partial x_n} \right)$

式が長いので数学のベクトル解析で用いられるハミルトン演算子 $\nabla$ のナブラを使って省略します。
$\displaystyle \nabla f = \left(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \cdots, \frac{\partial f}{\partial x_n} \right)$