はじめに
TensorFlow関連の記事を書いている割には、ディープラーニング(深層学習)について理解度が足りてないということもあって基礎的なところから理解してみようと思いました。幸い、ここ1年で本やブログ記事が増えてきたので助かります。
参考にした下記の2つ本となります。あと、この本の内容を元にした幾つかのブログの記事などです。
自分なりに理解したことをまとめて書いていきますが、詳細はリンク先を参照してください。
線形と非線形
機械学習をやる上で「線形」と「非線形」という言葉が出てきますので、先に説明しておきます。
線形
簡単に言えば、直線的な線のことです。
一次関数「例 y = ax + b」のように定数倍と足し算・引き算で表されたものとなります。
【追記 2017/07/21】
y = ax + bは、線形ではないとのことです、線形の定義では原点を通るとのこと。
そもそも線形ってどういうこと - Qiita
linear function 数学などに関する備忘録/ウェブリブログ
非線形
線形以外で曲線的や変化が激しい線のことです。
二次関数「例 y = x2」のように放物線などで表されたものです。
イメージ
左図が線形、右図が非線形となります。「★」と「○」を区分ける際に直線で区分けるのは簡単ですが、曲線的でないと区分けることが出来ないのは難しいです。
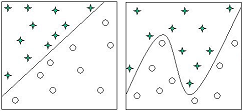
ディープラーニング(深層学習)とは
ディープラーニングは機械学習の一種で、神経細胞を模したパーセプトロン(ニューロンモデル)と言う小さな計算機をたくさん用意し多層にして構築したものです。よって、多層構造のニューラルネットワークを用いた機械学習と言えます。 ※パーセプトロンがニューラルネットワークの基本単位となります。
現在のディープラーニングに到るまでを順を追って書いています。
形式ニューロン
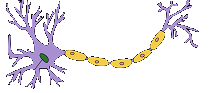
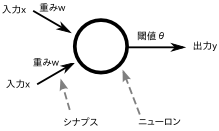
左図が本物の神経細胞(ニューロン) で、右図が形式ニューロンです。
形式ニューロンをWikipediaから引用します。
形式ニューロン(けいしきニューロン、英: formal neuron)や Threshold Logic Unit とは、1943年に神経生理学者・外科医であるウォーレン・マカロックと論理学者・数学者であるウォルター・ピッツが発表した最初の人工ニューロン(英: artificial neuron)[1]。伝達関数としてはヘヴィサイドの階段関数を使い、入出力の値は 0 または 1 の二値だけをとる。
簡単に説明すると、入力が2つあり各入力に対して重みが掛け算され、その値が閾値を超えれば出力は「1」、そうでなければ出力は「0」となります。 たとえば、入力が(1,0)、重みが(0.5, 0.7)だとすると、1×0.5 + 0×0.7 = 0.5 を計算して閾値と比較します。
形式ニューロンの場合、入力が「0」か「1」、重みが「実数」、出力が「0」か「1」となります。
パーセプトロン
心理学者のドナルド・ヘッブが、1949年に学習や記憶を進めるのは集中力や根性でなくシナプス(神経細胞同士の接合部)であると生理学的な提起をしました。「ヘッブの法則」というもので、シナプス(神経細胞同士の接合部)は、よく使うものほど強化され使わなくなると徐々に結合が弱くなります。
このヘップの法則を形式ニューロンのような神経回路モデルにあてはめることができないかということから考え出されたのが「パーセプトロン」となります。
単純パーセプトロン
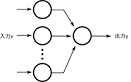
1958年にローゼンブラットが提案したパーセプトロンは形式ニューロンを発展させ、いくつか並列に組み合わせてから出力ニューロンで束ねるという2層(入力層と出力層)の構造をとることで、入力と出力のペアを学習することを示しました。
形式ニューロンと違う点としては、入力は「実数」であることと学習という過程があります。
トレーニングデータを複数を用意することによって、間違った答えを出力した場合、ある計算式に従って重みやバイアスの値を変化させます。
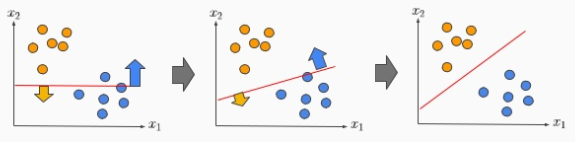
基本的には線型分離可能な問題しか解くことができない(ミンスキーとパパートにより指摘)という欠点があります。
余談ですが、ローゼンブラットが提案したパーセプトロンは非線形分離問題も扱える3層でしたが、その後の研究は中間層を省いた2層による単純パーセプトロンの研究が進んだため、ミンスキーとパパートの共著「パーセプトロン」(1969年出版)による批判も単純パーセプトロンだけに当てはまるものだったのです。パーセプトロンの熱は一気に冷めてしまい、パーセプトロンは線形分離可能問題しか扱えないというレッテルが貼られたのでした。
多層パーセプトロン
世の中の解きたい問題は大抵パーセプトロン(線型分離可能な問題)では解けないタイプの問題であったため、パーセプトロンの研究は廃れていきました。それ以降は人工知能の研究は学習型ではなく、知識を扱うプロダクションルール型に移行していった。
しかし、約15年後の1986年に認知心理学者ラメルハートが再発見した3層モデルのバックプロパゲーション(誤差逆伝播学習法)を発表したことで、再び脚光を浴びたのである。
再発見とは、1967年に甘利俊一先生が隠れ層のある3層以上の計算モデルを既に発表していた。
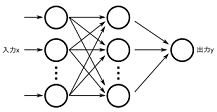
単純パーセプトロンに真ん中の層を追加しました。この層を隠れ層(hidden layer)または中間層と呼びます。実はこれだけで線形分離可能な問題しか解けないという欠点を解決できたのです。
単純パーセプトロンでは重みを調整するのが1層で簡単だったのですが、今回は2層でそれぞれの層の調整するのが難しという問題がありました。しかし、誤差逆伝搬(所望の出力結果になるよう誤差を出力層から入力層に向かった逆方向に重みを調整するもの)と呼ばれる方法を使うこと良い重みの調整方法を手に入れることができたため、3層構造でも学習可能になったのです。
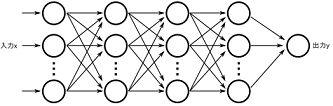
再びニューラルネットワークのブームが訪れ、あらゆるものに応用が試みられて3層より層を深くして学習効果を上げることも試されました。
しかし、バックプロパゲーションは4層以上にすると満足な精度が得られませんでした。
バックプロパゲーションを多層にすると勾配消失と過学習が発生することで、うまく学習できなくなるのです。
当時は、学習時間が非常にかかることや過学習を防ぐための理論がなく、サポートベクターマシン(SVM)など他の手法が注目されていたこともあり、再びニューラルネットワークは冬の時代を迎えたのでした。
ディープラーニング
冬の時代にも着々と進められた技術的進歩の中で、2006年にカナダのトロント大学のジェフリー・ヒントン教授が「ディープビリーフネットワーク」を発表した。これは層が深くなっても学習できていた。
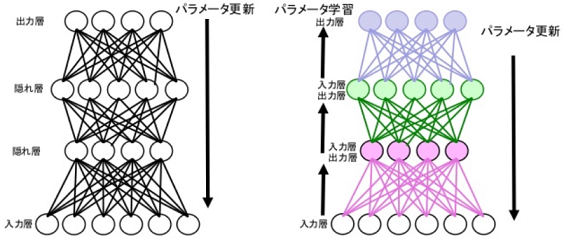
従来のニューラルネットワーク(左図)はパラメーターの更新を4層以上一度にやっていたが、ディープビリーフネットワーク(右図)では層毎に学習が完了してから次の層を付け足したことにある。1層が終わってから2層目と順に学習し、全ての学習が終わってから全層を結合してバックプロパゲーションをかけたのである。
2006年にヒントン教授の論文では層が深いニューラルネットを総称して「ディープネットワーク」と呼び、2007年にアンドリュー・ング氏が論文で「高次元データの階層的な表現の学習」に「ディープラーニング」という言葉を用いた。
2012年にアンドリュー・ング氏が畳込みニューラルネットワーク(CNN)で1000万本のYouTubeビデオ画像を学習し、ディープラーニングが学習した猫の画像を発表した。以降、ディープラーニングは爆発的なブームとなり、全てのものに応用が試みられるようになったのである。


現在のディープラーニングには「畳込みニューラルネットワーク」、「再起型ニューラルネットワーク」、「積層自己符号化器」、「ディープビリーフネットワーク」、「ディープボルツマンマシン」など多くの種類があります。
畳込みニューラルネットワーク(CNN)
現在、画像分類の分野で主流となっているのは「畳込みニューラルネットワーク(CNN)」です。この畳込みニューラルネットワークは、福島邦彦先生の「ネオコグニトロン」が元になっています。
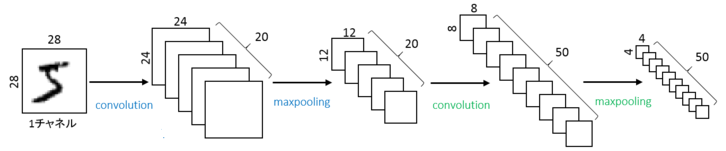
畳込みニューラルネットワークは、その名の通り畳込み(コンボリューション:Convolution)を行って情報を圧縮していくネットワークで、5層(入力層、畳込み層、プーリング層、全結合層、出力層)から構成されています。畳込み層とプーリング層は複数繰り返して深い層を形成し、その後の全結合層も同様に何層か続きます。
畳込み層では、カーネルという小さな正方形をフィルターとして適用しながら、入力された画像をより小さい画像に変換します。
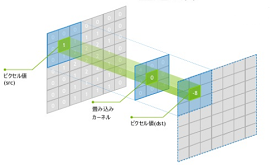
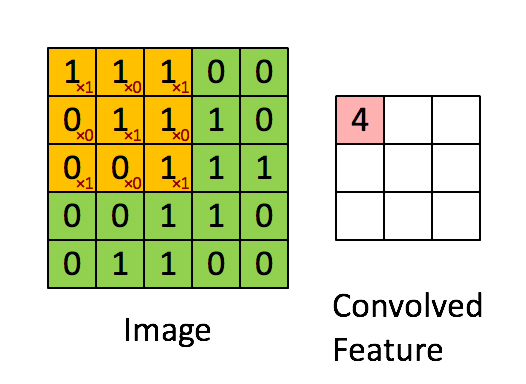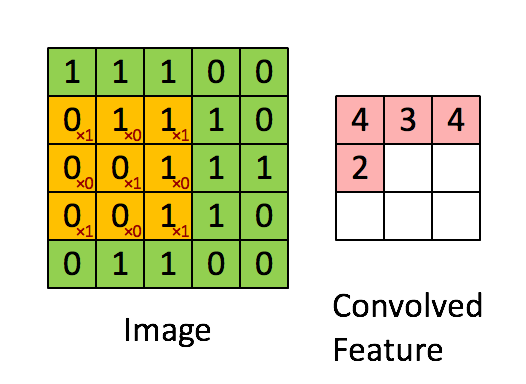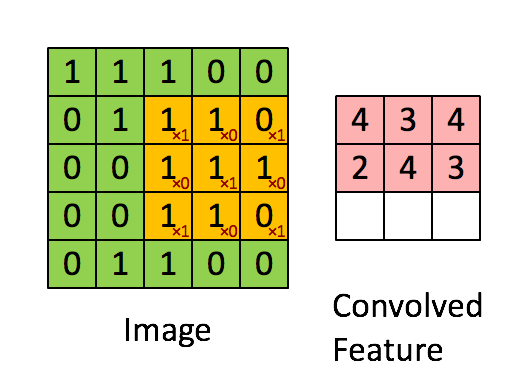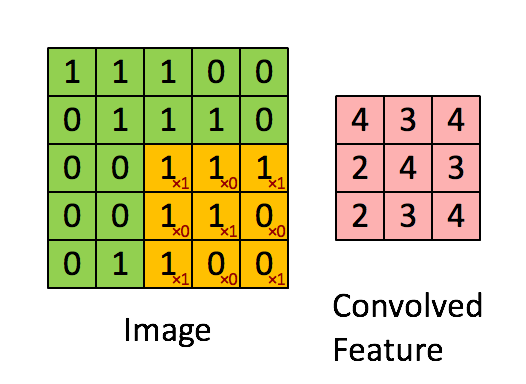
引用元:http://deeplearning.stanford.edu/wiki/index.php/Feature_extraction_using_convolution
プーリング層では、畳込み層から出力された特徴マップを縮小します。最大値プーリングの場合、注目領域の最大値を特徴マップの値とします。
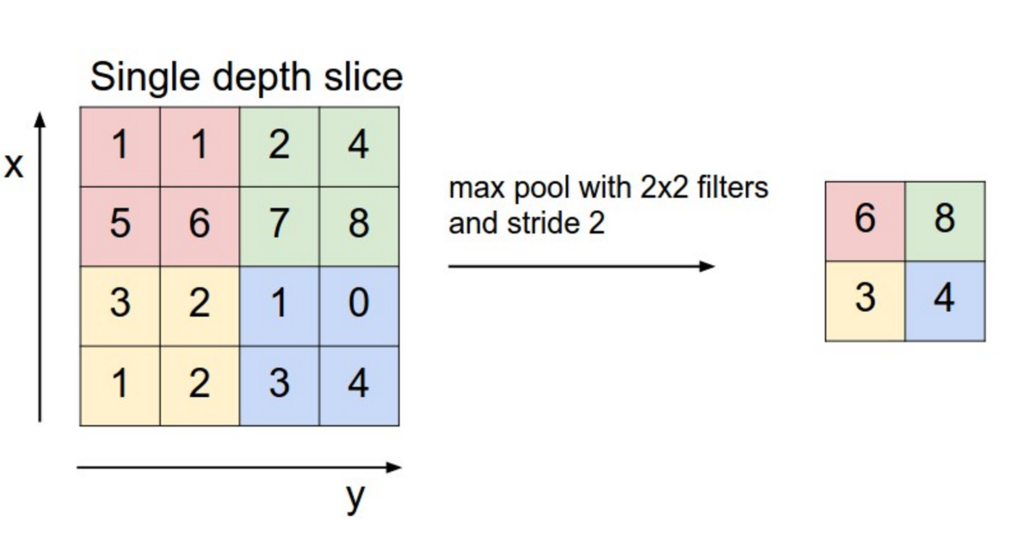
引用元: http://cs231n.github.io/convolutional-networks/#pool
画像認識での話ですが、プーリングは位置と回転に不変性を与えます。ある領域についてプーリングを行うと、画像が数ピクセルだけ移動や回転をしてもその出力はほぼ同じになります。それは最大プーリングが、微妙なピクセルの違いを無視して同じ値を抽出してきてくれるからです。
自然言語処理における畳み込みニューラルネットワークを理解する
浅いレイヤーは単純なパーツ(小さい部品より具体的なもの)を学習、深いレイヤーはパーツを組み合わせた全体の学習を行います。
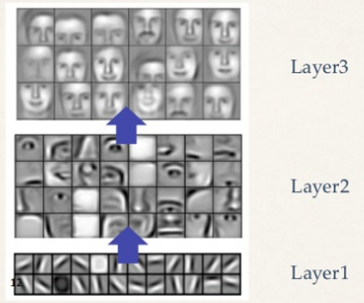
ネオコグニトロン
1979年に福島邦彦先生が後のディープラーニング計算に使われる「ネオコグニトロン」を発表した。現在のパターン認識を行うディープラーニングの構造は、ネオコグニトロンそのものであり、S細胞をコンボリューション、C細胞をプーリングと呼んでいるだけである。
ディープラーニングとの違いは学習の仕方で、ディープラーニングはバックプロパゲーションを採用しており、ネオコグニトロンは新しい入力パターンに反応する細胞がないときは新しく細胞を加えるという「add-if silent」学習則を採用している。
ネオコグニトロンは当初特許出願されていたものの、予算が厳しく特許権を放棄した。特許権を継続していれば今頃は莫大な収入を得ていたかも知れませんが、特許権が無いことでディープラーニングが開花したのかも。
パーセプトロンと論理演算
人間の脳は神経細胞(ニューロン)のネットワークで構成されています。この最小単位の神経細胞(ニューロン)を模倣したモデルがパーセプトロンとなります。このモデルは入力値が閾値を超えた場合に「1」を出力(この場合を「ニューロンが発火する」と表現)し、そうでない場合は「0」を出力します。このように入力値から出力値を生むまでの計算を活性化関数と呼びます。
活性化関数
活性化関数とはニューロンが入力から出力を生むまでの計算のことで、活性化関数には非線形関数が用いられます。線形の活性化関数では非線形分離できないためです。
パーセプトロンでは活性化関数にステップ関数(入力に対してある閾値を境に階段(ステップ)のように出力が1か0か決まる)を使っていた。

ニューラルネットワークは学習をする際に微分を含む計算を行うため、微分するとゼロになるステップ関数は都合が悪いことからシグモイド曲線(sigmoid)などが使用されている。
※微分するとゼロになると都合が悪いのは、値を微分値で更新しても同じ値のままになってしまうからです。
シグモイド曲線は入力した値を0から1の間に収めてくれる関数の1つです。多くの自然界に存在する事柄は、このようなS字曲線を取ります。欠点として1に近づくほど1そのものにならない性質があります。

論理演算
コンピュータの演算には四則演算(+、-、×、÷)のほかに論理演算(AND、OR、NOT、XOR)があります。論理演算とは、2つ以上の1または0入力値に対して、1つの演算結果(1または0)を出力する演算のことです。
論理演算と四則演算の大きな違いは、論理演算が2進数の1桁(=1bit)を対象としていることと、演算結果が決して桁上がりしないことです。コンピュータは、内部的にすべてのデータを2進数で取り扱っているからこそ、コンピュータの世界では論理演算が重要なのです。
清水亮著「はじめての深層学習(ディープラーニング)プログラミング」の「2.2 論理演算を学習をさせてみる」として、Chainerを使用して論理演算の「AND」と「OR」と「NAND」および「XOR」を学習させています。
※初版本を購入したため、ソースリストにも誤りがありました。参照:お詫びと訂正
前回の記事「Chainer ver2.xをWindowsにインストールしてみた」でChainerを入れたこともあって、そのまま利用しています。tensorflow版は「tensorflow 論理演算」で検索してみて下さい。
仕組みそのものを知りたい方は「ゼロから作るDeep Learning」の本が「Python + numpy」のみで説明しています。参照:ゼロから作るDeep Learning 2章「パーセプトロン」
#!/usr/bin/env python # coding: utf-8 import numpy as np import chainer.functions as F import chainer.links as L from chainer import Variable, optimizers,Chain class Model(Chain): def __init__(self): super(Model, self).__init__( l1 = L.Linear(2, 1), ) def __call__(self, x): # h = self.l1(x) # sigmoid function h = F.sigmoid(self.l1(x)) return h model = Model() optimizer = optimizers.MomentumSGD(lr=0.01, momentum=0.9) optimizer.setup(model) x = Variable(np.array([[0,0],[0,1],[1,0],[1,1]], dtype=np.float32)) # OR t = Variable(np.array([[0],[1],[1],[1]], dtype=np.float32)) # AND #t = Variable(np.array([[0],[0],[0],[1]], dtype=np.float32)) # NAND #t = Variable(np.array([[1],[1],[1],[0]], dtype=np.float32)) for i in range(0, 3000): optimizer.zero_grads() y = model(x) loss = F.mean_squared_error(y, t) loss.backward() optimizer.update() print("loss:", loss.data) print(y.data) #print(y.data.round())
「OR」の実行結果 四捨五入すれば上から[ 0, 1, 1, 1]となります。
︙ loss: 0.01094332616776228 loss: 0.01093930285423994 [[ 0.15879413] [ 0.90393192] [ 0.90352207] [ 0.99786234]]
このソースコードでは「OR」が実行されるようになっています。「AND」または「NAND」を実行するには対象コメントを外して、他のところは逆にコメントを付けてください。あと、急に「NAND」が出てきましたが何故かは後述します。
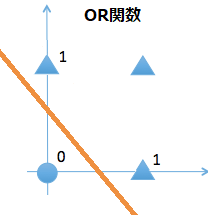
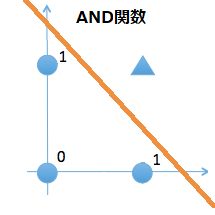
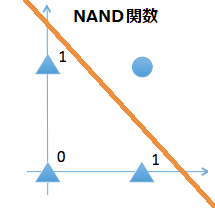
この中に「XOR」が無いのには理由があります。上図が示すように「OR」、「AND」、「NAND」については1本の判別直線で表現することが出来ます。つまり単純パーセプトロンで線型分離可能となっているわけです。
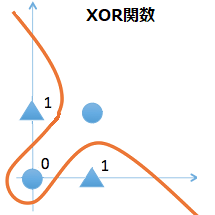
ところが「XOR」の場合は非線形(もしくは2本の判別直線)にしないと判別することが出来ません。
これを判別できるようにするには、単純パーセプトロンの中間層(隠れ層)を追加して多層パープセトロンにすればいいのです。
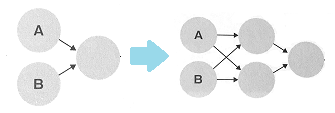
【2018/11/04追記】多重パーセプトロン <計算例> XOR回路を表現する
下記サイトのXOR回路をNAND回路とOR回路の2つに分ける(多重化)することで答えが求まるのが、分かりやすい。
arduinopid.web.fc2.com
修正したのは上側部分で変数l2の追加と変数tをXORに変更したくらいです。
#!/usr/bin/env python # coding: utf-8 import numpy as np import chainer.functions as F import chainer.links as L from chainer import Variable, optimizers,Chain class Model(Chain): def __init__(self): super(Model, self).__init__( l1 = L.Linear(2, 2), l2 = L.Linear(2, 1), ) def __call__(self, x): # sigmoid function h = F.sigmoid(self.l1(x)) return self.l2(h) model = Model() optimizer = optimizers.MomentumSGD(lr=0.01, momentum=0.9) optimizer.setup(model) x = Variable(np.array([[0,0],[0,1],[1,0],[1,1]], dtype=np.float32)) # XOR t = Variable(np.array([[0],[1],[1],[0]], dtype=np.float32)) for i in range(0, 3000): optimizer.zero_grads() y = model(x) loss = F.mean_squared_error(y, t) loss.backward() optimizer.update() print("loss:", loss.data) print(y.data) #print(y.data.round())
「XOR」の実行結果 四捨五入すれば上から[ 0, 1, 1, 0]となります。
︙ loss: 0.010527125559747219 loss: 0.01044147927314043 [[ 0.05130053] [ 0.8998214 ] [ 0.89989913] [ 0.13812399]]
NANDについて
余談ではあるのですが、「NAND」は「NOT + AND」の組合せたもので[ 1, 1, 1, 0]となります。
ソフトウェア側だとだから何だと思われるのですが、ハードウェア側の論理回路から見ると、すべての論理演算(OR,AND,NOT,XOR)はNAND回路を組み合わせれば出来てしまうのです。同様に「NOR」でもすべての論理演算が作れます。
詳しくは下記サイトを見て下さい。
最後に
脳を真似たモデルが最終的には凄い結果を出せるようになったわけで、生物って凄いなーとつくづく思います。
人間の身体全体が60兆個の細胞でできている中で、脳細胞は140億個と言われています。
PCのメモリ容量が2GB(160億ビット)として2値(0か1)なのでデータ量は2160億通り、脳のニューロンモデルが2値(発火しないか発火する)とすると2140億通りとすると、もう充分ではないかと思えるわけですが、実際はグリア細胞というニューロン細胞以外の神経細胞のために出力はディジタルではなくアナログ信号に近いとのことです。
生物は奥が深い。
この資料は良かったです。ディープラーニングが人工ニューロンから計算グラフに変わってきている。
参照
- ゼロから作るDeep Learningのメモまとめ
- 中学生にもわかるTensorFlow入門 その3 deepじゃないlearning - パーセプトロン
- 高卒でもわかる機械学習 (3) 多層パーセプトロン
- 【連載第1回】ニューラルネットの歩んだ道、ディープラーニングの登場で全てが変わった
- Convolutional Neural Networkとは何なのか
- ディープラーニング(7)
- Deep learningで画像認識③〜ネオコグニトロンとは?〜
- ハッカーの系譜(10)マービン・ミンスキー (9) 人工知能「冬の時代」が到来
- 【人工知能はいま 専門家に学ぶ】(5)情報幾何学の創始者、甘利俊一氏が見るAIの世界
- Deep Learningと画像認識 ~歴史・理論・実践~ - Slideshare
- 一般向けのDeep Learning - Slideshare

