はじめに

これは、機械学習に必要な高校数学やり直しアドベントカレンダー Advent Calendar 2016の10日目の記事です。

線形回帰ー誤差の和の式(データ個数 n 個の場合)

$\displaystyle E(\theta)=\frac{1}{2}\sum_{i=1}^{n}(y^{(i)}-f\theta(x^{(i)}))^2$

2乗することに関しては、以前書いた下記の記事にてピタゴラスの定理で距離を求めるという理解を得ることが出来ました。
正の数と負の数が混ざっていると都合が悪いから、必ず正の数にするために2乗するってことです。
それなら絶対値を取った値でもいいと思われるが、目的関数を微分することになった時に絶対値の微分より2乗の微分の方が簡単になる。
絶対値だと微分ができない場所があるのと、場合分けをしないといけないから面倒なのです。 yaju3d.hatenablog.jp

でも、全体を 2 で割ってる理由はなんだろうという疑問を持ちました。

経緯

「やる夫で学ぶ機械学習 - 単回帰問題 -」とgihyo.jpの「機械学習はじめよう第9回　線形回帰」も、全体を 2 で割る理由について、もやっとする感じな書き方なんです。

全体を 2 で割るのが、やる夫が言っているように「おまじない的なものは気持ち悪いお…、」なんです。本筋ではないので記事的に省略するのは仕方ないですけどね。

やる夫
全体を 2 で割ってるのは何だお？

やらない夫
後で E(θ) を微分することになるんだが、微分した式をちょっとだけ簡単にするためのトリックだ。最適化問題は、何か定数が全体に掛かっていたとしても、求まる答えは変わらないからこういうことができる。まあ、あまり深く考えなくていいさ。

やる夫
おまじない的なものは気持ち悪いお…、うーん、全体像はわかったけど、ちょっと、まだピンときてないお。
出典：やる夫で学ぶ機械学習 - 単回帰問題 -

ただし一般的な記法にあわせて，二乗和を2で割ったものを使います（注1）。
注1
2で割っていることは今回の範囲では全く本質的ではないのですが，次回以降の話との整合性のためにこの形式を用います。
出典：機械学習はじめよう第9回　線形回帰［後編］

調査

ネットで数時間かけて検索してみたのですが、ぜんぜん見つからないです(笑)。こういう時は人に頼るということで、 Yahoo!知恵袋に質問しました。

線形回帰の求め方で二乗和を2で割るの理由？ - 数学 | Yahoo!知恵袋

２人から回答をいただきました。その内の１人はブログに書き起こしくれました。勉強会で知り合った@K_Ryuichirouさんです。線形回帰の求め方で二乗和を2で割る理由 - Qiita

では、解決したのかというとそうではなく、理解する知識がまだ自分にはなかったのです、まずは微分を理解する必要があります。

理解

Yahoo!知恵袋のzatsugakusanさんの回答を一部抜粋すれば

例えば

f(x)=(x-1)²

を最小にするxを求めればx=1となりますが、

f(x)=100(x-1)²

を最小にするxを求めてもx=1になります。

二乗和の式をこれから微分すると分かっているのですから、微分して「２」が出てくることも予めわかっています。

ですから、二乗和の損失関数に1/2を掛けていれば微分したときに消えてくれるのでそうしておく。ただそれだけのことです。そうして求まるパラメータ自体には何の影響もありません。
「２で割るのは、単に二乗和が微分したら２が出てくることが分かっているからです。」

導関数の定義では、二次関数 $y=x^2$ を微分すると $y=2x$ になる。

参照：

この2を打ち消すということだが、まだピンとこない。

修正量による考え

修正された値を $x$ とし、2つの計測値を $a_1$ と $a_2$ とする。それぞれの計測値に修正を加える修正量を $v_1$ と $v_2$ とした場合、これらの間には「計測値＋修正量＝修正された計測値」の関係が成り立ち、これを数式にしてみる。

$a_1 + v_1 = x$

$a_2 + v_2 = x$

これらを修正量＝・・・の形式に書き換えます。

$v_1 = x - a_1$

$v_2 = x - a_2$

これを修正量の2乗の総和を S とすれば次のように計算できる。

$S = v_1^2 + v_2^2$

$= (x-a_1)^2 + (x-a_2)^2$

$= 2x^2 - 2(a_1+a_2)x + a_1^2 + a_2^2$

総和 S は、二次関数になるのでグラフが下向きの放物線になります。そして、放物線の頂点が最小値ということになります。総和 S を x で微分した上で「微分した値 = 0」とすれば目的の値を求めると次のような計算になります。

$\displaystyle \frac{dS}{dx}=4x-2(a_1+a_2)=0$

$\displaystyle 4x=2(a_1+a_2)$

$\displaystyle 2x=(a_1+a_2)$

$\displaystyle x=\frac{(a_1+a_2)}{2}$

f:id:Yaju3D:20161209030620p:plain

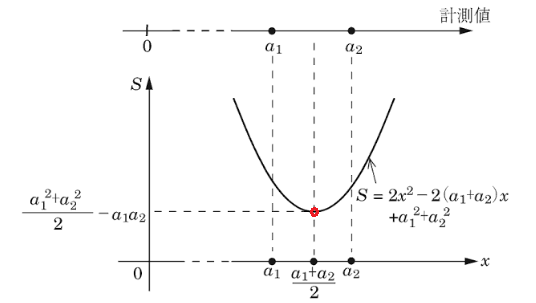
よって、最小値は図の赤丸のところで下記の式となる。

$\displaystyle x = \frac{(a_1+a_2)}{2}$

これは $a_1$ と $a_2$ の平均である。

でも、これは平均でたまたま2つだから2で割っただけで、3つになったら意味が違うかも知れない。

参照：わかりやすい測量の数学　―行列と最小二乗法― 著者: 小白井　亮一 Kindle版

微分係数とは何か

f(x)=(x-1)²

を最小にするxを求めればx=1となりますが、

f(x)=100(x-1)²

を最小にするxを求めてもx=1になります。

つまり、最小値に微分係数は関係ないようだ。そこで微分係数で検索していたら下記サイトを見つけた。

微分係数は、ある点における接線の傾きともいうことができます。虫めがねの図を思い出してください。
最小値をとるところ、つまり、ｘ＝０では接線の傾き（＝微分係数）はどうなりますか？
・・・接線は水平になりますね。
ということは、傾きは・・・　０ですね。
だから、微分係数が０になる点が最小値（ｙの値ですよ。）になるのです。

参照：６．微分の応用

結論

微分係数はある点における接線の傾きで最小値は水平となるので、微分係数は無視してｘ＝０を代入した値が最小値となる。

二乗和を微分したら微分係数に２が付くけど、微分係数は無視するので求まる答えは変わらない。
微分係数２は数式上は１／２を掛けて(2で割る)相殺しておくことが、数学として一般的な記法なっているということです。

最後に

これで、やらない夫の「何か定数が全体に掛かっていたとしても、求まる答えは変わらない」とYahoo!知恵袋のzatsugakusanさんの「２で割るのは、単に二乗和が微分したら２が出てくることが分かっているからです。」が分かったような気がします。

ただ、理解が間違っていたらご教示ください。

追記(2017/09/01)

実際に計算した結果をみると理解しやすいです。

yaju3d.hatenablog.jp 上記サイトでリンゴとミカンの最小値はリンゴ90円とミカン30円ですが、今回は求める上で2乗誤差の平均値を使ったので3で割っています。別に平均値ではなく合計値のままでもいいし、公式通りに1/2にしてもいいです。でも求まる最小値はリンゴ90円とミカン30円で結果は変わらない。数学の通例として公式では1/2にしているだけです。

追記(2019/03/24)

もう少しいい説明として下記の本を参考にしました。

今回の式は目的関数と呼ばれるもの。

$\displaystyle E(\theta)=\frac{1}{2}\sum_{i=1}^{n}(y^{(i)}-f\theta(x^{(i)}))^2$

$E(\theta)$ の $E$ は、誤差を英語で言った時の Error の値を文字から取っている。
この $E(\theta)$ の値が一番小さくなるような $\theta$ を見つけるのが目的で、こういうのを最適化問題という。

今回のように勝手に定数 $\displaystyle\frac{1}{2}$ を掛けてもの問題ないのは、誤差 $E$ を求めるのではなく最小値を求めるのが目的だから。

下図の $f(x)=x^{2}$ のグラフで左側の場合の最小値は $x=0$ 、定数を掛けた $f(x)=\displaystyle\frac{1}{2}x^{2}$ のグラフで右側の場合の最小値も同じように $x=0$ となる。
f:id:Yaju3D:20190324150422p:plain

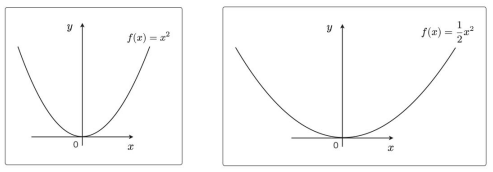
正の定数を掛けてもグラフの形が横に潰れたり縦に細くなるだけで、どこで最小値になるのかという場所は変わらない。
よって、 $f(x)=x^{2}$ を微分した時の微分係数 $2$ は数式上は $\displaystyle\frac{1}{2}$ を掛けて( $2$ で割る)相殺しておくことが、数学として一般的な記法なっている。