3Dを基礎から勉強する　カリング処理 - デジタル・デザイン・ラボラトリーな日々

前回、jsdo.itに投稿「３D入門３Dモデルを表示」したんですが、ある角度にすると欠けたような表示になっていて少し気にはしていたんです。

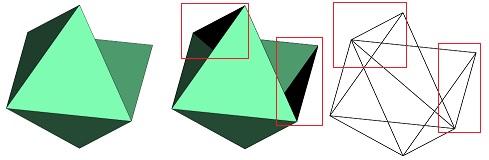
原因を調べると、奥行きの小さい順に描画しているが、裏面の方が奥行きが大きくなる面があり、その部分が黒色で表示されてしまい、一部が欠けたような表示となっていたのです。下図では赤枠で囲んだ部分で、ワイヤーフレームにすると分かりますが、裏面の三角形が食い込んでいるところが対象です。

左がカリング後、中央がカリング前、右がカリング前のワイヤーフレーム

f:id:Yaju3D:20140906161940j:plain

上図のモデルが複雑な形をしているので、簡単な立方体で表してみました。

f:id:Yaju3D:20140906172350j:plain

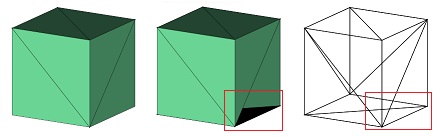
今回、表面だけ表示するカリング処理を追加することで、左図のように正常なモデルが表示されます。

以前、フラットシェーディングの記事を書いた時にも立方体を表示しましたが、この時は１面を四角形のまま描画していたので、この問題は発生しなかったのです。1面を三角形の2つの組み合わせで描画したことでカリングする必要が出てきたのです。

カリングする判定方法として下記の2通りがあるが、今回は勉強のために1を採用した。

三角形頂点の配置順序で判定(時計回り以外なら描画しない)
法線ベクトルの値

■1.三角形頂点の配置順序で判定

３Dモデルを作成する際の各三角形の頂点の配置順序を予め統一しておきます。

今回は表向きを時計回りとして説明します。

そうすると表側が時計回りということは、裏側は反時計回りということになります。

f:id:Yaju3D:20140906192235j:plain

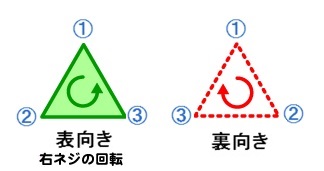
今回判定で使っている isFace(p1:Point, p2:Point, p3:Point)では

下記にて判定しています。

$(x_2 -x_1)(y_3 -y_1) \gt (x_3 -x_1)(y_2 -y_1)$ 反時計回りなら、-1

$(x_2 -x_1)(y_3 -y_1) \lt (x_3 -x_1)(y_2 -y_1)$ 時計回りなら、1

それ以外は直線 0

月の杜工房 - ポリゴンに対する内外の判定を参考に作ったわけですが、これはどういうことなんだろうと思って調べてみると、どうも外積の考えを使っています。

$x_a=(x_2 -x_1)$ 　 $y_a=(y_2 -y_1)$ 　 $x_b=(x_3 -x_1)$ 　 $y_b=(y_3 -y_1)$

$\vec{a} = \left( \begin{array}{c} x_a \\ y_a \end{array} \right)$ 　 $\vec{b} = \left( \begin{array}{c} x_b \\ y_b \end{array} \right)$ とすると、以下の様に表現できます。

$\vec{a} \times \vec{b} = x_a y_b - y_a x_b$

判定するだけなので、両辺を引き算処理せずに不等号で判定しています。

そもそも、外積って何だって方は、以前書いた記事を参考にしてください。

3Dを基礎から勉強する外積 - デジタル・デザイン・ラボラトリーな日々

外積では、sinθが求まります。

下図を見てもらうと分かりますが、sinは±180度以上でマイナスの値になります。
外積の結果の符合を見ることで左右が分かります。

f:id:Yaju3D:20130526151945j:plain

※ポリゴンのどちらを表側と定義するかについて

・右手座標系のOpenGLでは視点から見て反時計回りだと表
・左手座標系のDirectXでは視点から見て時計回りだと表
とされています。参照：ポリゴンの表裏の判定方法

■2.法線ベクトルの値

元々のプログラムにはフラットシェーディングする際の面の明るさ用に法線ベクトルの値(face.nz)が求まっていました。その値を使って0未満ならで裏として描画しないようにします。
裏表を法線ベクトルで判定
if (face.nz < 0) continue

そもそも、法線ベクトルって何だって方は、以前書いた記事を参考にしてください。

3Dを基礎から勉強する外積 - デジタル・デザイン・ラボラトリーな日々

法線ベクトルのz成分がcosθとなり、下図を見てもらうと分かりやすいですが、0値(90度)以降は表面、0値(90度)未満は裏面となります。

f:id:Yaju3D:20130525230936j:plain

※法線ベクトルのz成分だけでいいのは、z軸の正の方向から原点に向かって平行光源が当たっているものとしているためです。それ以外の方法ではもう少し計算式が必要。

参照:3Dモデルを表示するJavaアプレットの作成（2/3）：CodeZine

■z座標が0のベクトルの外積
V1=(10,20, 0) 、V2=(30,40,0)のようにz成分が0とした場合、ベクトルがxy平面上にあることになり、その外積のベクトルはz軸と平行になるため、z成分に値が求まります。
$\vec{a}=(10,20,0)$ , $\vec{b}=(30,40,0)$ 　とすると　
$\vec{a} \times \vec{b} = \mid (20\times0 - 0\times40),(0\times30 - 10\times0),(10\times40 - 20\times30) \mid$
$\vec{a} \times \vec{b} = \mid (0),(0),(-200) \mid$
これは、2次元ベクトルの外積の結果と3次元ベクトルの外積のz成分の結果が同じとなります。