主成分分析という言葉を知ったのは、昨年に静岡Developers勉強会で「入門機械学習」の第8章のセッション担当をしたことである。
静岡Developers勉強会では、読書会形式で勉強会を行っており、講師は固定せずにメンバー内で章ごと担当を決めて講師をするといった形式で行っています。第8章が株による説明であった為、株に興味があった私が担当することにしました。ただ調べながら作成したものの、いまいち理解が出来ないまま参考にしたスライドやWebサイトでそれなりに纏めて作成したのが、下記のスライドになります。
今年は静岡Developers勉強会で「コンピュータビジョン」を行っております。この中でも主成分分析が何回か出てきます。第3章が画像間の写像であり、このブログでも射影変換の記事を書いていたこともあり、この章は私が担当しました。当時は主成分分析について軽く書いた程度でしたが、もう少し調べなおして追記したのが現在のスライドになります。
静岡Developers勉強会の「コンピュータビジョン 3章 画像間の写像」の資料公開
今回の記事の内容としては、スライドから主成分分析のところを抜き出して説明を少し追記する形になります。
数式を使わないで現時点で私が理解できたところまでを書きます。理解が違うところがありましたら、コメントを頂ければ修正していきます。
■主成分分析
主成分分析は英語では PCA(Principal Components Analysis)といいます。その為、ライブラリ上のメソッド名には「pca」が使われます。
主成分分析の目的は大きく2つあります。
・データを新しい視点でみるための新しい軸を見つける
・大きいデータの情報をできるだけ損わずに小さい情報を落とす
主成分分析の目的の1つである新しい軸の見方について
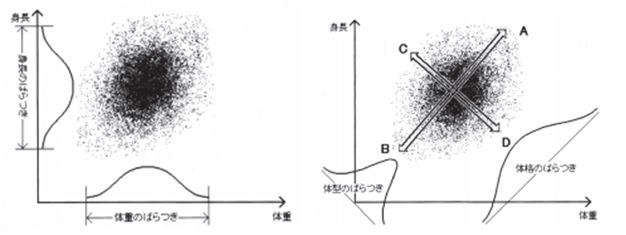
例えば、「身長」と「体重」という 2つのデータから人間の体つきについて分析したとする。
ばらつきを身長方向や体重方向で考えるのではなく、
下図右に示したA-BとC-Dの方向で考えた場合、 Aの向きは身長・体重がともに大きいことからA-B方向は、いわば「体格」を示す。 Cの向きは身長が高い割に体重が軽い(やせ型)ことから、直行するC-D方向は「体型」を示すといえる。
方向からデータの持つ情報を効率的に記述し、理解することができる。
似たような例でもう一つ、5教科(数学、理科、国語、英語、社会)の25人分のテスト結果があった場合、主成分分析をすると第1主成分に総合成績が得られ、第2主成分に理系科目/文系科目という軸が現れます。
下図では、丸印が優秀な生徒で四角が優秀でない生徒、塗り潰しは理系向き、白抜きは文系向きを表しています。

一般的に数学の得点が高い人は理科の得点が高く、国語の得点が高い人は社会や英語の得点が高いといった相関関係があることから、理系(数学と理科)と文系(国語、社会、英語)にグループ分けを予めしてあります。
しかし、このようにグループ分けが最初から分かるような分析ばかりではありません。主成分は第一、第二だけではなく、第三、第四、第五など指定しただけ成分を出すことが出来ます。主成分の軸を出したが、それがどういう意味を持っているのかは分析した人間側が考えて答えを導き出す必要があります。
先ほど主成分は指定しただけ成分を出せると書きましたが、全ての成分が重要ではありません。重要な成分かどうかは寄与率をみます。例えば、第一主成分の寄与率が0.65あった場合、第1主成分だけで、元データが持つ情報の約65%を説明していると読み取れます。もし第3主成分の寄与率が0.1しかない場合には第一主成分と第二主成分だけで考えればいいのです。
主成分分析は、分散共分散行列に対応させる方法と相関係数行列に対応させる方法の二種類の方法が存在します。
【データ】 → 【共分散】 → 【相関】
と相関係数の計算途中に共分散は算出されます
相関係数行列の対応させる方法のみ説明します。
例えば、片方が重さで片方が長さというように違っている場合は、g と m がよいのか、kg と cm がよいのか判断できません。
そこで各変量を標準化済み(平均 0、分散 1)に変換することで、もとのデータがどんな単位で測定されていても、常に同じように主成分分析をすることができます。
■主成分スコア(得点)
5教科のテストの合計得点で順位を出してしまうと公平とは言えないことがあります。
例えば、国語の平均が30点(SD 10),数学の平均点が70点(SD 20)であった場合
-国語が得意なA君は国語が40点、数学が50点で、2教科の合計は90点。
-数学が得意なB君は国語が20点、数学が90点で、2教科の合計は110点。
単に足しあわせた合計得点には、数学の得点の影響がより大きく反映してしまう。
数学が得意な学生が上位を占め、国語が得意な学生の順位が低くなってしまうことになり、あまりフェアなやり方とはいえません。
主成分分析を用いることで、各教科の重み付け係数が求まります。
この重み付け係数を使って合成得点を算出することで公平な順位を出すことできます。
主成分スコア = 国語の点数 × 国語の重み係数 + 数学の点数 × 数学の重み係数・・・
次回は、次元の縮約について書きます。
【参考】
コーヒーの「コク」「香り」「酸味」のデータから新たな評価軸を生み出すには? Excelで相関係数行列、固有値と固有ベクトルを求める (1/6):MarkeZine(マーケジン)
コーヒーの「コク」「香り」「酸味」のデータから新たな評価軸を生み出すには? Excelで相関係数行列、固有値と固有ベクトルを求める (1/6):MarkeZine(マーケジン)