【コンピュータビジョン】3章「画像間の写像」　ホモグラフィ - デジタル・デザイン・ラボラトリーな日々

今年の静岡Developes勉強会は「O'Reilly Japan - 実践コンピュータビジョン」を課題図書として学んでいる。4/12に行われる「静岡Developers勉強会コンピュータビジョン vol.3」では3章「画像間の写像」について勉強する。
3章ではホモグラフィーやアフィン変換などがあり、当ブログで射影変換やテクスチャマッピングについて書いてきたこともあって、発表者として立候補して担当することとなった。

ホモグラフィーは、ある平面から別の平面へ写像する2Dの射影変換である。
$\begin{pmatrix}x'\\y'\\w'\end{pmatrix}= \begin{pmatrix}h1&h2&h3\\h4&h5&h6\\h7&h8&h9\end{pmatrix} \begin{pmatrix}x\\y\\w\end{pmatrix}$
すなわち $x'=Hx$

本にはホモグラフィー行列を $H$ (h1～h9)を求める方法としてDLTアルゴリズム(Direct Linear Transform)を使っている。これは私が当ブログで調べてきた方法と違うため、当初かなり混乱した。
DLTアルゴリズムを理解する上で、下記サイトが役に立った。

私がこれまで学んできた方法は、4つの点の対応を使って8次元連立一次方程式にて $H$ を解いていました。参照：射影変換(ホモグラフィ)について理解してみる

DLT(Direct Linear Transform：直接線形変換)法は、4つ以上の点の対応を使って $H$ を計算するアルゴリズムです。
点数の2倍の行を持つ下記の行列式(2nx9)に展開します。
f:id:Yaju3D:20140329231943j:plain
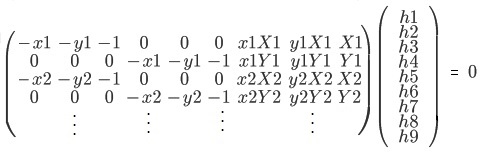
下図は、8つの点に対応した場合である。この場合、n=8となり2x8 x9の行列となる。
f:id:Yaju3D:20140329172305j:plain

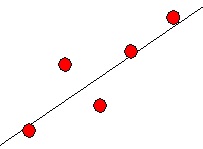
点が増えた場合、最小二乗法を使って解くことになります。最小二乗法は下図のように複数の点があった場合に直線で近似 $y=ax+b$ を求める方式で、誤差の二乗が最小になる直線が最良近似とします。
f:id:Yaju3D:20140329180804j:plain $\displaystyle E(a,b)=\sum_{i=1}^n (y_i-ax_i-b)^2$
誤差の二乗の和の式 $E(a,b)$ は、 $a$ にも $b$ にも2次式でその係数は正の値なので最小値がある。
誤差 $E$ の最小値は、それぞれ偏微分した値がゼロとなるときに得ることが出来る。
これは、 $a$ と $b$ の連立方程式である。