前回は25にメッシュ分割して表示することが出来た。
今回は各メッシュの部分をマウスで動かせるようにツールを作成してみる。
前回の猫画像では小さ目なので、ネットで猫のイメージ検索してみました。
今回テクスチャで使用するのは、このかわいい猫ちゃんです。

前々回で4つの点をマウスで動作させるツールは作成しているので、これを25の点に拡張させればいいわけです。
作成している途中で気が付いたのですが、25の点だと20面と一周り小さいんですよね。25面に対して動作させるには点の数は(5+1)*(5+1)で36点必要でした。
表示の基となるのは、drawTriangle関数ですね。
function drawTriangle(g, img, vertex_list, uv_list)
vertex_listは、描画する三角形の頂点座標3つである。
uv_listは、テクスチャの頂点座標3つである。UV座標は0~1の範囲で指定する。
各赤い制御点(marks)の変更により、vertex_listのの座標を変更しても、テクスチャ座標であるuv_listは制御点(marks)によって変更されることは無いんです。
//テクスチャ描画 function drawTexture(){ var ctx = cvs.ctx; var m = mesh; //mesh=5 var mm = mesh + 1; var wx = texture.width / m; var wy = texture.height / m; //marksの配列の並び順 // 0 1 2 3 4 5 // 6 7 8 9 10 11 //12 13 14 15 16 17 //18 19 20 21 22 23 //24 25 26 27 28 29 //30 31 32 33 34 35 for(var i=0; i<m; i++){ for(var j=0; j<m; j++){ drawTriangle(ctx, texture.image, [ marks[i*mm+j].x, marks[i*mm+j].y, marks[i*mm+(j+1)].x, marks[i*mm+(j+1)].y, marks[(i+1)*mm+j].x, marks[(i+1)*mm+j].y ], [ j/m, i/m, (j+1)/m, i/m, j/m, (i+1)/m ] ); drawTriangle(ctx, texture.image, [ marks[(i+1)*mm+j].x, marks[(i+1)*mm+j].y, marks[(i+1)*mm+(j+1)].x, marks[(i+1)*mm+(j+1)].y, marks[i*mm+(j+1)].x, marks[i*mm+(j+1)].y ], [ j/m, (i+1)/m, (j+1)/m, (i+1)/m, (j+1)/m, i/m, ] ); } } }
今回は各制御点の座標は隣同士くっついているのですが、三角形ごとにそれぞれ座標を分ければ、下記のサイトのように粉砕するアニメーションも可能になるでしょう。
Delaunay triangulation(ドロネー三角形分割)
http://wonderfl.net/c/cjBf
また、各格子にバネの要素を追加すれば、下記サイトのようにプヨプヨしたアニメーションを作れたりする。
Flashでグニグニ曲がるUIを作る方法
http://sipo.jp/blog/2010/07/flashui.html
上記サイトについては、3D関連を一通りを学んだ後にでも、挑戦しようと思っています。
さて、各制御点をマウスを使って動作させることが出来ました。
前回のツール同様に、角度を指定した回転の実装もしたいところです。
4隅の回転だけなら前回のルーチンで簡単に出来たのですが、それだと各隅4点のみが回転して他の31点が回転しないから、当然変な画像になるわけです。
回転処理ルーチンは以前から下記を使用しているので、ここに変更は無い。
function rotate2d(x, y, rad) { var p = new Point; p.x = Math.cos(rad) * x - Math.sin(rad) * y; p.y = Math.sin(rad) * x + Math.cos(rad) * y; return p; }
これを36点全てに対して行えばいいはずですが、やはり回転の原理をちゃんと理解していないから悩んでしまうんだよね。
参考にしている「入門グラフィックス」の本を見直してみると、回転中心を原点に移動→原点で回転後にもとに戻すとなっている。
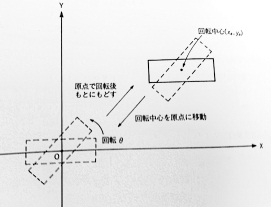
回転中心の座標は、画像の中心(texture.width / 2 , texture.height / 2)、現在の表示位置をoffsetとしている。
回転させる座標(vertexs)に対し画像の中心とオフセット値を減算し原点(0,0)に移動、回転後の座標に画像の中心とオフセット値を加算している。
var degrees = newValue; var rad = -degrees / 180 * Math.PI; var ct = new Point(texture.width / 2 , texture.height / 2); var sx = offset.x; var sy = offset.y; for(var i=0; i<marks.length; i++){ var pt = rotate2d(vertexs[i].x - sx - ct.x, vertexs[i].y - sy - ct.y , rad); marks[i].x = pt.x + sx + ct.x; marks[i].y = pt.y + sy + ct.y; }
ちなみに回転させる座標(vertexs)は、始めに制御点の座標をセットしている。
//回転用に退避 for(var i=0; i<marks.length; i++){ pt = new Point(marks[i].x, marks[i].y); vertexs.push(pt); }
これで角度を変更させることで回転させることが出来た。
次は、画像を波のように揺らすようにします。
これは、参考にしたテクスチャの下記のサンプルが2つとも揺らしているので、これはやっておくの流儀と思ってます。
http://jsdo.it/hidetaro7/triangle01
http://jsdo.it/edo_m18/aOuH
画像を揺らすには、正弦波(sin)を使います。横に揺らすので、x座標に対して行います。
正弦波については、下記サイトにアニメーションがあります。
http://www.osaka-kyoiku.ac.jp/~masako/exp/kichu/experiment/theory/seigenha.html
式 = 振幅(w) × sin(周期(T) × Y値 + 位相(a))
//揺らす処理 function drawWave(s){ if(!document.getElementById("waveCheck").checked) return; //揺れスピード if(speed >0 && s % speed != 0) return; var m = mesh; var mm = mesh + 1; var wx = texture.width / m; var wy = texture.height / m; var t,w,a; //周期(T) 波が1回上下するのにかかる時間を「周期(T)」波の高さ t = Math.PI*2 / cycle; //振幅(w) 波の高さ w = swing; //位相(a) 一周期内の波の位置 a = s % 5; for(var i=0; i<mm; i++){ for(var j=0; j<mm; j++){ //X座標 = 振幅(w) × sin(周期(T) × Y値(i) + 位相(a)) marks[i*mm+j].x = w * Math.sin(t*i+a) + j * wx + offset.x; marks[i*mm+j].y = i * wy + offset.y; } } }
上記を踏まえてツールを作成してみました。
See the Pen
テクスチャメッシュツール by やじゅ (@yaju-the-encoder)
on CodePen.