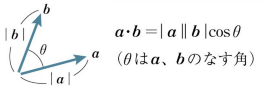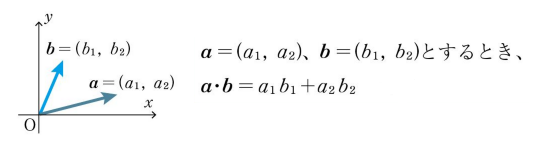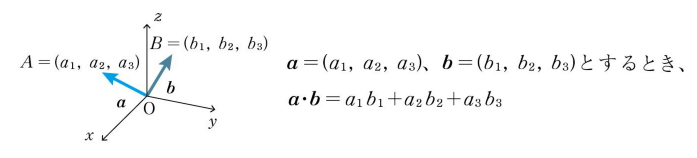2018-01-01

「サザエさんのじゃんけんデータ分析」の2017年の結果

機械学習

はじめに

明けましておめでとうございます。

昨年も東芝に暗雲が立ち込め、東証2部に降格して日経平均から外れ、ついには18年3月末にサザエさんからのスポンサー契約を降板する方向で調整とあいなりました。
さて、サザエさんのじゃんけんを長年記録しデータをWebスクレイピングさせて頂いた「サザエさんジャンケン学」が2017年6月25日を以て終了されていました。データを取得した際に7月以降がなかったので、あれっと思って見たらそういうことでした。長い間お疲れ様でしたm(_ _)m
www.asahi-net.or.jp

さてさて、2017年のサザエさんのじゃんけん結果はどうなったでしょう。ちなみに、2016年のサザエさんのじゃんけん結果は、27勝11敗12分(勝率0.711)でした。

人工知能による予測化を断念

本来はDeepLearningを使用して予想をする予定でしたが、まだ勉強中のままです。あと少しだと思うので今年中にはなんとかなると思います。
昨年、R言語からPythonに切り替えました。
qiita.com

Python使うに際にはいつも Jyupter notebook だったので、この為に久しぶりに Visual Studio Code で Python を実行しようとしてバージョンアップ(1.19.1)したらタスク実行の設定がいろいろ変わって動かなくて、四苦八苦しながらなんとか動かせるようにしました。下記の記事を修正してあります。 yaju3d.hatenablog.jp

次の手の予測アルゴリズム

チョキが多いので、グー＞チョキ＞パーの優先順位とする
前回と違う手を出すので、上記の優先順位で勝手を選ぶ
二手前と一手前が違う手なら、残りの手を出すので勝手を選ぶ
三手の中に同手がある場合、残りの手を出すので勝手を選ぶ
二手前と一手前が同じ手なら、勝手を出すので負手を選ぶ

2017年の勝敗結果

年月	サザエさんの手	予想の手	勝敗結果
01月01日	休み
01月08日	チョキ	グー	勝ち
01月15日	チョキ	グー	勝ち
01月22日	パー	パー	引き分け
01月29日	グー	パー	勝ち
02月05日	グー	グー	引き分け
02月12日	パー	グー	負け
02月19日	チョキ	グー	勝ち
02月26日	チョキ	パー	負け
03月05日	グー	パー	勝ち
03月12日	パー	チョキ	勝ち
03月19日	休み
03月26日	チョキ	グー	勝ち
04月02日	チョキ	パー	負け
04月09日	グー	パー	勝ち
04月16日	パー	チョキ	勝ち
04月23日	パー	グー	負け
04月30日	チョキ	グー	勝ち
05月07日	グー	パー	勝ち
05月14日	パー	チョキ	勝ち
05月21日	チョキ	グー	勝ち
05月28日	グー	パー	勝ち
06月04日	チョキ	チョキ	引き分け
06月11日	パー	チョキ	勝ち
06月18日	グー	パー	勝ち
06月25日	グー	グー	引き分け
07月02日	チョキ	グー	勝ち
07月09日	パー	チョキ	勝ち
07月16日	グー	パー	勝ち
07月23日	パー	グー	負け
07月30日	チョキ	グー	勝ち
08月06日	パー	パー	引き分け
08月13日	グー	パー	勝ち
08月20日	チョキ	グー	勝ち
08月27日	グー	チョキ	負け
09月03日	パー	チョキ	勝ち
09月10日	パー	グー	負け
09月17日	チョキ	グー	勝ち
09月24日	グー	パー	勝ち
10月01日	チョキ	チョキ	引き分け
10月15日	パー	チョキ	勝ち
10月22日	グー	パー	勝ち
10月29日	休み
11月05日	チョキ	グー	勝ち
11月12日	チョキ	チョキ	引き分け
11月19日	グー	チョキ	負け
11月26日	パー	チョキ	勝ち
12月03日	パー	グー	負け
12月10日	チョキ	グー	勝ち
12月17日	グー	パー	勝ち
12月24日	パー	チョキ	勝ち

結果は、32勝9敗7分(勝率0.780)となりました。

ちなみに、サザエさんじゃんけん研究所公式ウェブサイトのサザエさんの手の予想と勝負結果(2017年)が29勝8敗11分(勝率0.783)でした。

今回は勝数では上回ったのですが、勝率では僅差で負けました。勝率の計算は、「勝ち / (勝ち + 負け)」で行っているのですが、負けの1つが響いたわけです。

【2017/01/09追記】
２０１７年冬版サザエさんじゃんけん白書によるとクール(四半期)の初回(1月、4月、7月、10月の初回)はチョキが出やすいとのことです。もし、これを取り入れた場合、04月02日(負け)と10月01日(引き分け)なので、34勝8敗6分(勝率0.809)になるかな。

年	データ分析	研究所公式
2013	24勝13敗12分(勝率0.649)	25勝9敗17分(勝率0.735)
2014	30勝10敗11分(勝率0.750)	30勝9敗12分(勝率0.769)
2015	32勝9敗9分(勝率0.780)	33勝9敗8分(勝率0.785)
2016	27勝11敗12分(勝率0.711)	22勝13敗15分(勝率0.628)
2017	32勝9敗7分(勝率0.780)	29勝8敗11分(勝率0.783)

スライド

2013年に静岡Developers勉強会で機械学習を学び、2014年1月にネタとしてSlideShareに公開しました。

サザエさんのじゃんけん　データ分析 from yaju88

最後に

今年中にはTensorFlowを使って人工知能のディープラーニングで予測手を作りたいと思います。まだ組むだけの理解度(n-gramモデル)が足りないためですが、あと少しで理解度が進むはずです。

【2018/01/07 追記】
r_stdさんが、機械学習を用いて検証してくれました。2016年に統計検定準1級に合格している方で幾つかの手法を使っています。その中で、naive bayesで33勝9敗6分と好成績を残しています。タイトルが①なので次回も期待しています。
r-std.hatenablog.com

2017-11-28

ディープラーニング(深層学習)を理解してみる(勾配降下法：計算確認)

機械学習 tensorflow 人工知能

はじめに

前回の続きです。 yaju3d.hatenablog.jp

前回の計算が本当に合っているのか、Pythonを使って実証してみたいと思います。

プログラム

重みの更新

①現在の重みで推測値を求める

import numpy as np
a = np.array([10, 20])
b = np.array([[1,3,5],[3,1,7]])
print(np.dot(a,b))

[ 70, 50, 190]

全体の誤差を求める。
二乗誤差は、mean_squared_error の名前です。

def mean_squared_error(y, t):
    return 0.5 * np.sum((y - t)**2)

y = np.array([70, 50, 190])
t = np.array([190, 330, 660])

print(mean_squared_error(y, t))

156850.0

②勾配 $\Delta E$ を計算する
勾配は、gradient の名前です。転置は x.T とTを付けるだけなんですね。

def gradient(y, t, x):
    return np.dot((y - t),x.T)
    
t = np.array([190, 330, 660])
y = np.array([70, 50, 190])
x = np.array([[1,3,5],[3,1,7]])

print(gradient(y, t, x))

[-3310 -3930]

③重みを更新する
②で求めた勾配 $\Delta E$ を用いて、現在の重み $w$ を更新します。学習係数 $η$ は 0.02 としています。

def weight(w, lr, gd):
    return w - lr * gd

t = np.array([190, 330, 660])
y = np.array([70, 50, 190])
x = np.array([[1,3,5],[3,1,7]])
w = np.array([10, 20])

print(weight(w, 0.02, gradient(y, t, x)))

[ 76.2 98.6]

2回目の①現在の重みで推測値を求める

a = weight(w, 0.02, gradient(y, t, x))
b = np.array([[1,3,5],[3,1,7]])
print(np.dot(a,b))

[ 372. 327.2 1071.2]

全体の誤差を求める。
二乗誤差は、mean_squared_error の名前です。

y = np.dot(a,b)
t = np.array([190, 330, 660])

print(mean_squared_error(y, t))

101108.64

というのを繰り返す。

import numpy as np

# 二乗誤差を求める
def mean_squared_error(y, t):
    return 0.5 * np.sum((y - t)**2)

# 勾配を求める
def gradient(y, t, x):
    return np.dot((y - t),x.T)

# 重みを求める
def weight(w, lr, gd):
    return w - lr * gd

# 教師データ
t = np.array([190, 330, 660])
# 重み
w = np.array([10, 20])
# 入力データ(個数)
x = np.array([[1,3,5],[3,1,7]])
y = None
for i in range(100):
    if y is not None:
        # 勾配を求める
        grad = gradient(y, t, x)
        # 重みを求める
        w = weight(w, 0.02, grad)
    # 推測値を求める
    y = np.dot(w, x)
    # 誤差を求める
    l = mean_squared_error(y, t)
    if (i + 1) % 10 == 0:
        print("step=%3d, a1=%6.2f, a2=%6.2f, loss=%.2f" % (i + 1, w[0], w[1], l))
print("Estimated: a1=%6.2f, a2=%6.2f" % (w[0], w[1]))

step= 10, a1= 78.84, a2= 48.86, loss=4531.39
step= 20, a1= 89.41, a2= 32.85, loss=564.82
step= 30, a1= 94.92, a2= 27.91, loss=264.21
step= 40, a1= 97.30, a2= 26.05, loss=217.63
step= 50, a1= 98.28, a2= 25.30, loss=209.89
step= 60, a1= 98.68, a2= 25.00, loss=208.59
step= 70, a1= 98.84, a2= 24.88, loss=208.38
step= 80, a1= 98.91, a2= 24.83, loss=208.34
step= 90, a1= 98.94, a2= 24.81, loss=208.33
step=100, a1= 98.95, a2= 24.80, loss=208.33
Estimated: a1= 98.95, a2= 24.80

実行結果
リンゴ 98.95 ≒ 99、ミカン 24.80 ≒ 25 → 99 x 2 + 25 x 4 ≒ 297

以前、TensorFlowで組んだ際の結果とほぼ同じになったのでこれでいいかな。
リンゴ 98.81 ≒ 99、ミカン 24.90 ≒ 25 → 99 x 2 + 25 x 4 ≒ 297
yaju3d.hatenablog.jp

上記サイトでTensorFlowで組んだのに近付けるために、train_x と train_y を縦ベクトルに変更してみました。

f:id:Yaju3D:20160419005112p:plain f:id:Yaju3D:20160419002003p:plain

import numpy as np

# 二乗誤差を求める
def mean_squared_error(y, t):
    return 0.5 * np.sum((y - t)**2)

# 勾配を求める
def gradient(y, t, x):
    return np.dot((y.T - t.T), x)

# 重みを求める
def weight(w, lr, gd):
    return w - lr * gd

train_x = np.array([[1., 3.], [3., 1.], [5., 7.]])
train_y = np.array([190, 330, 660]).reshape(3, 1)
y = None
for i in range(100):
    if y is not None:
        # 勾配を求める
        grad = gradient(y, train_y, train_x)
        # 重みを求める(横ベクトルを一次元に変換)
        w = weight(w, 0.02, grad).reshape(-1,)
    else:
        # 初期重み
        w = np.array([10, 20])

    # 推測値を求める
    y = np.dot(w, train_x.T)
    # 誤差を求める
    l = mean_squared_error(y, train_y)
    if (i + 1) % 10 == 0:
        print("step=%3d, a1=%6.2f, a2=%6.2f, loss=%.2f" % (i + 1, w[0], w[1], l))
print("Estimated: a1=%6.2f, a2=%6.2f" % (w[0], w[1]))

2017-10-11

ディープラーニング(深層学習)を理解してみる(勾配降下法：計算方法)

機械学習 tensorflow 人工知能

はじめに

前回の続きです。 yaju3d.hatenablog.jp

幾つかの人工知能関連の本やWebサイトを見ても、数式やプログラムのソースリストは記載されていても、数学が苦手な自分が理解できるようになるまでの説明が無い、そんな中でも下記3つの本(Kindle)がまだ理解できそうな感じで参考になりそうである。

基礎的な知識から、やっと実際の計算方法に入っていきます。

勾配降下法

関数 $z=x^2 + y^2$ について、その最小値を与える $x$ と $y$ の値を勾配降下法で求めてみます。
ちなみに、正解は $(x, y)=(0, 0)$ です。
f:id:Yaju3D:20171028224142p:plain

最初に勾配を求めておきましょう。
前回記事の偏微分で説明したように、関数 $z=x^{2} + y^{2}$ を偏微分すると指数を係数にした $\displaystyle\frac{\partial z}{\partial x}=2x$ 、 $\displaystyle\frac{\partial z}{\partial y}=2y$ となります。

①勾配式　 $\displaystyle\left(\frac{\partial z}{\partial x}, \frac{\partial z}{\partial y} \right) = (2x, 2y)$

それでは、ステップを追って計算を進めます。

１.初期設定

初期位置と学習係数 $\eta$ を適当に与えます。
今回は初期位置を(3.00,2.00)、学習係数 $\eta = 0.1$ とします。

No	位	置	勾	配	変位ベ	クトル	関数値
i	$x_i$	$y_i$	$\partial z / \partial x$	$\partial z / \partial y$	$\Delta x$	$\Delta y$	$z$
0	3.00	2.00

２．変位ベクトルを算出

現在位置 $(x_i, y_i)$ に対して、勾配式から算出し、勾配降下法の基本式から変位ベクトル $\Delta x = (\Delta x_i, \Delta y_i)$ を求めます。
前回記事の勾配降下法に適用で、2変数関数 $z=f(x,y)$ の勾配降下法の基本式は次のように表しました。
基本式 $\displaystyle({\Delta x}, {\Delta y}) = -\eta\nabla f(x,y)$

これに①勾配式を当てはめたのが次の式となります。「 $\cdot$ 」は掛け算の意味です。
②変位ベクトル $(\Delta x_i, \Delta y_i) = - \eta(2x, 2y) = (- \eta\cdot2x, - \eta\cdot2y)$

No	位	置	勾	配	変位ベ	クトル	関数値
i	$x_i$	$y_i$	$\partial z / \partial x$	$\partial z / \partial y$	$\Delta x$	$\Delta y$	$z$
0	3.00	2.00	6.00	4.00	-0.60	-0.40	13.00

各計算結果の求め方

勾配
$\partial z / \partial x = 2 \cdot x_0 = 2 \times 3.00 = 6.00$
$\partial z / \partial y = 2 \cdot y_0 = 2 \times 2.00 = 4.00$
変位ベクトル
$\Delta x = - \eta \cdot \partial z / \partial x = -0.1 \times 6.00 = -0.60$
$\Delta y = - \eta \cdot \partial z / \partial y = -0.1 \times 4.00 = -0.40$
関数値
$z = x_0^2 + y_0^2 = 3.00^2 + 2.00^2 = 9.00 + 4.00 = 13.00$

３．位置を更新

勾配降下法に従って、現在位置 $(x_i, y_i)$ から移動先 $(x_{i+1}, y_{i+1})$ の点を次の式から求めます。
②移動先 $(x_{i+1}, y_{i+1}) = (x_i, y_i) + (\Delta x_i, \Delta y_i)$

No	位	置	勾	配	変位ベ	クトル	関数値
i	$x_i$	$y_i$	$\partial z / \partial x$	$\partial z / \partial y$	$\Delta x$	$\Delta y$	$z$
0	3.00	2.00	6.00	4.00	-0.60	-0.40	13.00
1	2.40	1.60

移動先
$x_1 = x_0 + \Delta x_0 = 3.00 + (-0.60) = 2.40$
$y_1 = y_0 + \Delta y_0 = 2.00 + (-0.40) = 1.60$

４．２と３の繰り返し

２と３の繰り返し(6～27は省略)、30回繰り返したときの座標 $(x_{30}, y_{30})$ の値です。
正解の $(x, y) = (0, 0)$ と一致します。

No	位	置	勾	配	変位ベ	クトル	関数値
i	$x_i$	$y_i$	$\partial z / \partial x$	$\partial z / \partial y$	$\Delta x$	$\Delta y$	$z$
0	3.00	2.00	6.00	4.00	-0.60	-0.40	13.00
1	2.40	1.60	4.80	3.20	-0.48	-0.32	8.32
2	1.92	1.28	3.84	2.56	-0.38	-0.26	5.32
3	1.54	1.02	3.07	2.05	-0.31	-0.20	3.41
4	1.23	0.82	2.46	1.64	-0.25	-0.16	2.18
5	0.96	0.66	1.97	1.31	-0.20	-0.13	1.40
28	0.01	0.00	0.01	0.01	0.00	0.00	0.00
29	0.00	0.00	0.01	0.01	0.00	0.00	0.00
30	0.00	0.00	0.01	0.00	0.00	0.00	0.00

※Excel計算で小数誤差により微妙に値が違います。

バイアスについて

バイアス(bias)とは、一般に真値からの偏り、つまり系統的な誤差を指す。

切片(せっぺん)

ニューラルネットワークのパラメーターは重みとバイアスがセットとなります。
バイアスがイメージしやすいものとして、回帰直線があります。
f:id:Yaju3D:20171105230836p:plain
回帰直線は次のような1次式で表現されます。
回帰方程式 $y = ax + b$
f:id:Yaju3D:20171106001201p:plain
a を回帰係数(傾き)、bを切片の呼びます。切片が無いと必ず原点を通すことになってしまいます。
傾きが求まったところで切片で上下位置の調整をします。この切片がバイアスのことになります。

閾値(しきいち)

f:id:Yaju3D:20170528144340p:plain f:id:Yaju3D:20170528154127p:plain
左図が本物の神経細胞(ニューロン) で、右図が形式ニューロンです。
簡単に説明すると、入力が2つあり各入力に対して重みが掛け算され、その値が閾値を超えれば出力は「1」、そうでなければ出力は「0」となります。たとえば、入力が(1,0)、重みが(0.5, 0.7)だとすると、1×0.5 ＋ 0×0.7 ＝ 0.5 を計算して閾値と比較します。
閾値未満だと出力無し(発火なし)、閾値を超えると出力有り(発火あり)となります。

出力信号無し $(y=0):w_1x_1+w_2x_2 \lt \theta$
出力信号有り $(y=1):w_1x_1+w_2x_2 \geqq \theta$

ここで $\theta$ はニューロン固有の閾値です。 $\theta$ を左に移行させた発火の式は次のように表現することができます。
発火の式 $y=a(w_1x_1+w_2x_2 - \theta)$
※ $a$ は活性化関数となります。

活性化関数にシグモイド曲線を使った場合の閾値 $\theta$ は生物的にはニューロンの個性を表現する値です。
$\theta$ が大きければ興奮しにくく(すなわち鈍感)、小さければ興奮しやすい(すなわち敏感)という感受性を表します。
f:id:Yaju3D:20171106013953p:plain

発火の式 $y=a(w_1x_1+w_2x_2 - \theta)$ にて、 $\theta$ だけマイナス記号が付いているのは数学的に美しくありません。美しさが欠けることは数学が嫌うところです。また、マイナスは計算ミスを誘発しやすいという欠点を持ちます。そこで、 $-\theta$ を $b$ と置き換えたのが次の式となります。
$y=a(w_1x_1+w_2x_2 + b)$
こうすれば式として美しく、計算ミスも起こりにくくなります。
この $b$ をバイアス(bias)と呼びます。

バイアスの式表現

数式では b とするよりは $w_0$ として、次の式にします。
$y=a(w_0 + w_1x_1+w_2x_2)$

一般的に書き直すと、重みを $w$ ではなく $\theta$ として、 $\theta_0$ をバイアスとした場合、入力値 $x$ とすると $\theta_0$ と $x$ で次元が違うと扱いにくいので、最初の要素に $1$ をセットする。
f:id:Yaju3D:20180103202510p:plain

それを $x_0=1$ と定義して、 $x$ の最初の要素に $x_0$ を置くほうがより数学上では綺麗となる。
f:id:Yaju3D:20180103210343p:plain

$\theta$ を転置したものと $x$ を掛けたものを計算すると次の式になります。
$\theta^Tx = \theta_0x_0 + \theta_1x_1+ \theta_2x_2 + \cdot + \theta_nx_n$
更にこれを書き直すと、 $f_\theta(x) = \theta^Tx$ と簡易的な表現の式となる。

やる夫で学ぶ機械学習 - 多項式回帰と重回帰 - · けんごのお屋敷

リンゴとミカン

リンゴとミカンを例題に勾配降下法を計算していきます。上記と違うのは、訓練データがあることです。 f:id:Yaju3D:20160417230234p:plain
f:id:Yaju3D:20160419005112p:plain f:id:Yaju3D:20160419002003p:plain

以前の記事を参考にします。
yaju3d.hatenablog.jp

前提

f:id:Yaju3D:20171029165625p:plain
1層の全結合ニューラルネットワークを用いて、勾配降下法による重みの更新例を示します。
入力層ユニット数は2、出力層はユニット数が1のシンプルなネットワークです。損失関数は二乗誤差を用います。

No	入力	データ	教師データ
i	$x_1$	$x_2$	$t$
1	1	3	190
2	3	1	330
3	5	7	660

上表はトレーニングデータセットです。サンプル数は3で、1番目のサンプルを見ると、 $x_1=1$ 、 $x_2=3$ が与えられたときの教師データ $t=190$ (正解)になっています。

勾配 $\Delta E$ の計算式

出力層の出力値 $y$ は、入力層の出力値 $x$ を用いて、次のような一次多項式で表すことができます。
$a_1x_1+a_2x_2+b=y$
パラメーター　 $a_1,a_2,b$

これにトレーニングデータセットを当てはめると、次のような連結方程式が出来上がります。
$a_1+3a_2+b=y_1$
$3a_1+a_2+b=y_2$
$5a_1+7a_2+b=y_3$

この連結方程式は行列とベクトルを用いて次のように表すことが出来ます。

  
    w　　　　　X　　　　   Y
   重み　　入力データ　出力データ(推測値)

今回はバイアスbは 0 とするので除外しました。そうしないリンゴとミカンの金額(重み)を求めたいのにバイアスを含む3つ値が求まってしまいます。

  
    w　　　　　X　　　　   Y
   重み　　入力データ　出力データ(推測値)

誤差を含めた式と行列を表現すると下記のようなります。
$y=a_1x_1 + a_2x_2 + 誤差 e$

入力データを $X$ 、重み(パラメーター)を $w$ 、出力データ(推測値) $Y$ としています。 $w$ と $X$ を用いると、出力データ $Y$ は次の式で表すことができます。
$wX=Y$
また、教師データは、 $t$ を用いて次のように表します。
$t=(190 \quad 330 \quad 660)$

損失関数には二乗誤差を使用します。誤差は次のような式で表すことができます。
$E=\displaystyle \frac{1}{2} (Y - t)^2$
$\quad=\displaystyle \frac{1}{2} (wX - t)^2$
勾配 $\Delta E$ は、誤差 $E$ を重み $w$ で微分すると、勾配 $\Delta E$ を次のような式になります。
$\Delta E = \displaystyle \frac{\partial E}{\partial w} = (Y - t)X^T$
$X^T$ ： $X$ の転置行列、 $(Y - t)$ ：誤差信号 $\delta$

今回、 $(Y - t)$ を誤差信号と呼び、記号 $\delta$ (デルタ)で表します。
勾配 $\Delta E$ は、誤差信号 $\delta$ と、入力データ $X$ から求めることができます。入力データはすでにわかっている値なので、誤差信号の値を求めれば、勾配 $\Delta E$ を求めることができ、そして勾配 $\Delta E$ がわかれば、式 $w \leftarrow w-\eta\Delta E$ で重みを $w$ を更新することができます。 $\eta$ ：学習係数

初期値の設定

初めに、重み $w$ と学習係数 $\eta$ に適当な初期値を設定します。ここでは学習係数 $\eta$ は 0.02 とし、重み $w$ の初期値を10円と20円から、バイアスは 0 にして次のように設定します。
$w=(a_1 \quad a_2) = (10 \quad 20)$

重みの更新

①～③の手順で重みの更新を行います。

①現在の重みで推測値を求める

入力データ $X$ と現在の重み $w$ から、推測値 $Y$ を求めます。
推測値

ここで、全体の誤差をいったん計算してみます。損失関数には二乗誤差を使用するので、全体の誤差 $E$ は次のように計算します。

現在の値
教師データ $t=(190 \quad 330 \quad 660)$
推測値　　 $Y=( 70 \quad 50 \quad 190)$
全体の誤差
$E=\displaystyle \sum_{n=1}^{3} \frac{1}{2}(y_n - t_n)^2$
$\quad=\displaystyle \frac{1}{2}(y_1 - t_1)^2 + \frac{1}{2}(y_2 - t_2)^2 + \frac{1}{2}(y_3 - t_3)^2$
$\quad=\displaystyle \frac{1}{2}(70 - 190)^2 + \frac{1}{2}(50 - 330)^2 + \frac{1}{2}(190 - 660)^2$
$\quad=\displaystyle \frac{1}{2}(-120)^2 + \frac{1}{2}(-280)^2 + \frac{1}{2}(-470)^2$
$\quad=\displaystyle 7200 + 39200 + 110450$
$\quad=\displaystyle 156850$

②勾配 $\Delta E$ を計算する

現在の重み $w$ に対する勾配 $\Delta E$ を計算します。
入力データを転置行列 $X^T$ にするのは、行列の掛け算の定義で「行列Aの列数(横の個数)と、行列Bの行数(縦の個数)が等しくないと掛け算できない」ためです。
行列A( $Y-t$ ) 1行3列と行列B( $X^T$ ) 3行2列にして掛け算させます。行列の積

現在の値
教師データ $t=(190 \quad 330 \quad 660)$
推測値　　 $Y=( 70 \quad 50 \quad 190)$

入力データ　  

勾配

③重みを更新する

②で求めた勾配 $\Delta E$ を用いて、現在の重み $w$ を更新します。学習係数 $\eta$ は 0.02 としています。

現在の値
現在の重み $w=(10 \quad 20)$
勾配　　 $\Delta E=(-3310 \quad -3930)$
更新後の重み
$w \leftarrow w-\eta\Delta E$
$\quad=(10 \quad 20) - 0.02 \times (-3310 \quad -3930)$
$\quad=(10 \quad 20) - (-66.2 \quad -78.6)$
$\quad=(10 - (-66.2) \quad 20 - (-78.6))$
$\quad=(76.2 \quad 98.6)$

これで重み $w$ が更新されました。ここで、更新後の重み $w$ を使って推測値を求め、全体の誤差を再び計算してみます。

現在の値
教師データ $t=(190 \quad 330 \quad 660)$

推測値

全体の誤差
$E=\displaystyle \sum_{n=1}^{3} \frac{1}{2}(y_n - t_n)^2$
$\quad=\displaystyle \frac{1}{2}(y_1 - t_1)^2 + \frac{1}{2}(y_2 - t_2)^2 + \frac{1}{2}(y_3 - t_3)^2$
$\quad=\displaystyle \frac{1}{2}(372 - 190)^2 + \frac{1}{2}(327.2 - 330)^2 + \frac{1}{2}(1071.2 - 660)^2$
$\quad=\displaystyle \frac{1}{2}(182)^2 + \frac{1}{2}(-2.8)^2 + \frac{1}{2}(411.2)^2$
$\quad=\displaystyle 16562 + 3.92 + 84542.72$
$\quad=\displaystyle 101108.64$

全体の誤差は 101108.64 となり、重みの誤差前の 156850 より小さくなっていることが分かります。

更新の繰り返し

以上の①～③の計算で、全サンプル(今回は2サンプル)の更新が1回終わりました。これで1エポックを終了したことになります。
更新後の重み $w$ を用いて、①～③をもう一度繰り返せば、2エポックが終了となります。

最後に

計算の繰り返しはコンピューターの得意なところです。
次回はこの計算が本当に合っているのか、Pythonを使って実証してみたいと思います。

2017-09-26

ディープラーニング(深層学習)を理解してみる(勾配降下法：ベクトル、内積、微分、偏微分)

機械学習 tensorflow 人工知能

はじめに

前回の続きです。 yaju3d.hatenablog.jp

計算方法に入る前にベクトル等の基礎知識を先に説明していきます。

ベクトル

ベクトルとは大きさと向きを持つ量と定義されます。
f:id:Yaju3D:20171001213101p:plain

ベクトルの矢を座標平面上に置くことで座標のように表現できます。矢の始点を原点に置き、矢の終点の座標でそのベクトルを表します。これをベクトルの成分表示といいます。
成分表示されたベクトル $a$ で下図のように表現します。また3D座標上でもz軸方向を追加して同じように表現します。
f:id:Yaju3D:20171001225146p:plain

下図のように矢印がたくさんある図を見たことがありませんか?
各データは、どこかの一点のデータを基準にして、大きさと向きを持つベクトルとなります。
f:id:Yaju3D:20171001213359p:plain

内積

ベクトルにも足し算と引き算があるように掛け算も…といいたいところですが、微妙に違うのが内積です。内積だとベクトル同士を掛け算っぽくするのに結果はベクトルではなくスカラという1つの値となります。内積以外にも外積がありますが、ここでは説明しません。

過去に3Dの勉強用に書いた記事がありますので、興味があれば読んでみて見ください。

なぜ内積の計算をそうするのかは次のサイトの説明が分かりやすいと思います。
www.yukisako.xyz

内積というのは2つのベクトルの“近さ”を表しているという程度に理解しておけばいいです。
2つのベクトルの近さを表すのに $cos\theta$ が使われます。

f:id:Yaju3D:20171001231022p:plain

高校までの数学だと「内積の値が $cos\theta$ を使って表される」と教わるが、逆に「 $cos\theta$ の値が内積によって定義されるのだ」と考えるようにするといいでしょう。

$cos\theta$ の値は2つのベクトルの向きが反対なら「-1」、同じであれば「1」となる。 f:id:Yaju3D:20171002005747p:plain

（ア）2つのベクトルが反対向きのときに内積は最小値
（イ）2つのベクトルが平行でないとき、内積は平行の場合の中間の値
（ウ）2つのベクトルが同じ向きのときに内積は最大値

そして、（ア）の内積が最小値というのが、勾配降下法の基本原理となります。

手書き数字認識でどの数字か分類できるのは、より似ているかで判断しています。
方向が似ているベクトルを「似ている」と判断するなら、2つのベクトルが似ていると内積は大きくなるのです。
f:id:Yaju3D:20171002005805p:plain

内積の計算

平面(2次元)
f:id:Yaju3D:20171002005819p:plain

立方空間(3次元)
f:id:Yaju3D:20171002005835p:plain

内積は2次元や3次元に限らず、何次元のベクトルについても計算することができます。現実世界では4次元や10次元ベクトルで表せるものは存在しないですが、数学上は計算できるところが数学のおもしろいところでもあります。

この内積が何次元(多次元)であっても計算できるということが重要なポイントです。
リンゴとミカンの値段を求める際は2変数です、それにブドウを付け加えると3変数になり、レモンも付け加えると4変数になります。変数が多くなることを多変数と言います。この多変数というのは機械学習における多次元と同じ意味を持っています。

参照

微分

微分とは、ある関数の各点における傾き(変化の割合)のことです。
そして勾配降下法においては、傾きの最小値を求めることが目的です。 f:id:Yaju3D:20171007211313p:plain

最小値

微分において、傾きが水平になる 0 が最小値といいたいところですが、下図右のように最大値においても水平になり 0 となります。
f:id:Yaju3D:20171008132102p:plain

このことは、勾配降下法においては厄介な性質になります。
f:id:Yaju3D:20170917223314p:plain

導関数

関数 $y=x^{2}$ を微分して得られた導関数は指数を係数にした ${y}'=2x$ となります。
微分の定義式では極限の記号 $\displaystyle \lim_{h \to 0}$ を使って、x の変化量 h を限りなく 0 に近づけます。

$\displaystyle \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}={f}'(x)$

※現代の数学では、0 で割る(分母が0)ことは禁止事項とされているので、極限まで 0 に近づければいいという屁理屈です。

ちなみに、 $'$ の名称は「プライム」で、 $\lim$ の名称は「リミット」と読み、極限(limit)を取る記号です。

https://sci-pursuit.com/math/differential-1.htmlsci-pursuit.com

偏微分

関数 $y=x^{2}$ は変数が1つでしたが、リンゴとミカンの値段を求める場合は2変数による関数 $z=f(x,y)$ となります。このように変数が2つ以上の関数を多変数関数といいます。
多変数関数でも微分法を適用できます。ただし変数が複数あるので、どの変数について微分するかを明示しなければなりません。この意味で、ある特定の変数について微分することを偏微分(partial derivative)といいます。
例えば、2変数x，yから成り立つ関数を考えてみましょう。変数xだけに着目してyは定数と考える微分を「xについての偏微分」と呼び、次の記号で表します。

$\displaystyle\frac{\partial z}{\partial x}=\frac{\partial f(x,y)}{\partial x}=\lim_{x \to 0}\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}$

yについての偏微分も同様です。

$\displaystyle\frac{\partial z}{\partial y}=\frac{\partial f(x,y)}{\partial y}=\lim_{y \to 0}\frac{f(x,y+\Delta y)-f(x,y)}{\Delta y}$

ちなみに、 $\partial$ の名称は「デル」、 $\Delta$ の名称は「デルタ」です。

関数 $z=x^{2} + y^{2}$ を偏微分すると指数を係数にした $\displaystyle\frac{\partial z}{\partial x}=2x$ 、 $\displaystyle\frac{\partial z}{\partial y}=2y$ となります。

remedics.air-nifty.com

www.youtube.com

勾配降下法に適用

上述で説明してきたベクトルと内積と偏微分が勾配降下法にどのように使われるのか？

勾配降下法は、少しずつ下りながら、場所ごとに最も急な勾配を探すことになります。
$P0$ から最も勾配の急な点 $P1$ の位置を求める。その位置 $P1$ から更に最も勾配の急な点 $P2$ の位置を求める。このように繰り返すことで最も早く最小点にたどり着くようになります。 f:id:Yaju3D:20170924211620p:plain

関数 $z=f(x,y)$ において、xをΔxだけ、yをΔyだけ変化させたとき、関数 $z=f(x,y)$ の変化は下記式となります。
$\displaystyle \Delta z = f(x + {\Delta x},y + {\Delta y}) - f(x,y)$
これを近似公式から次の関係が成立します。
$\displaystyle \Delta z = \frac{\partial f(x,y)}{\partial x}{\Delta x} + \frac{\partial f(x,y)}{\partial y}{\Delta y}$

f:id:Yaju3D:20171010235143p:plain

そして、これは2つのベクトルの内積を表す式になっているのです。 f:id:Yaju3D:20171010234406p:plain

ベクトルが反対向きになっている時に、内積が最小値となっている。 f:id:Yaju3D:20171011001024p:plain f:id:Yaju3D:20171011001230p:plain

ベクトルが反対向きは、 $-1$ となり、勾配降下法の基本式は次のように表せます。( $\eta$ は正の小さな定数)
$\displaystyle({\Delta x}, {\Delta y})=-\eta\left(\frac{\partial f(x,y)}{\partial x}, \frac{\partial f(x,y)}{\partial y} \right)$

ちなみに、 $\eta$ はイータと読むギリシャ文字です。ローマ字のiに対応します。
なぜループカウンタ変数のほとんどに “i”が使用されるのか？ - Qiita

重要なのは、内積は何次元(何変数)のベクトルについても計算することができます。

$\displaystyle({\Delta x_1}, {\Delta x_2}, \cdots, {\Delta x_n})=-\eta\left(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \cdots, \frac{\partial f}{\partial x_n} \right)$

式が長いので数学のベクトル解析で用いられるハミルトン演算子 $\nabla$ のナブラを使って省略します。
$\displaystyle \nabla f = \left(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \cdots, \frac{\partial f}{\partial x_n} \right)$

2変数関数 $z=f(x,y)$ の勾配降下法の基本式は次のように表せます。
$\displaystyle({\Delta x}, {\Delta y}) = -\eta\nabla f(x,y)$

3変数関数 $z=f(x,y,z)$ の勾配降下法の基本式は次のように表せます。
$\displaystyle({\Delta x}, {\Delta y}, {\Delta z}) = -\eta\nabla f(x,y,z)$

次回は計算方法について説明していきます。

参照

2017-08-27

ディープラーニング(深層学習)を理解してみる(勾配降下法：最急降下法と確率的勾配降下法)

機械学習 tensorflow 人工知能

はじめに

前回の続きです。 yaju3d.hatenablog.jp

勾配降下法をどうして使うのかは理解できたのですが、その計算方法がまだ理解が足りてなくて、微分の本とかを読んでいました。
数学は苦手なんですが、理解はしたい。おまじないとかそういうルールだからとかで済ましたくないんですよね。

勾配降下法の他にも最急降下法とか確率的勾配降下法の用語がありますので、この違いも理解したい。
今回は下記の本(Kindle)を参考にしている。

勾配降下法

f:id:Yaju3D:20170917211137p:plain
勾配には、傾斜の程度・斜面という意味があります。
上図では1変数による関数 $y=f(x)$ でグラフは放物線となります。

リンゴとミカンの値段を求める場合は2変数による関数 $z=f(x,y)$ となり下図のようにワイングラスの底のような形になります。ちなみに3変数以上は図で表わすのは困難です。
f:id:Yaju3D:20170924173848p:plain
下図は関数のグラフの一部を拡大し、斜面に見立てた図となります。その斜面上のある点Pにピンポン玉を置き、そっと手を放すと玉は最も急な斜面を選んで転がり始めます。
f:id:Yaju3D:20170924181321p:plain

この操作を何回も繰り返せば、ピンポン玉は最短な経路をたどってグラフの底、すなわち関数の最小値にたどり着くはずです。この玉の動き(誤差関数という坂道、つまり「勾配」を下へ下へと「降下」していく)を真似たのが勾配降下法です。
f:id:Yaju3D:20170924183956p:plain

正確には最小値を探す場合を勾配降下法(gradient descent mothod)と言い、最大値を探す場合を勾配上昇法(gradient ascent mothod)と言います。descentは、SQLで降順にソートさせる時に略称(desc)で、order by column descと使いますね。

最短で下るには、少しずつ下りながら、場所ごとに最も急な勾配を探すことになります。
$P_0$ から最も勾配の急な点 $P_1$ の位置を求める。その位置 $P_1$ から更に最も勾配の急な点 $P_2$ の位置を求める。このように繰り返すことで最も早く最小点にたどり着くようになります。
f:id:Yaju3D:20170924211620p:plain

数値解析の分野では勾配降下法を最急降下法と呼びますが、勾配降下法の中にもいくつかの方法が存在します。

最急降下法(Gradient Descent) ※デフォルト
確率的勾配降下法（Stochastic Gradient Descent - SDG）
ミニバッチ確率的勾配降下法（Minibatch SGD - MSGD）

最急降下法とは

最急降下法は学習データのすべての誤差の合計を取ってからパラメーターを更新します。学習データが多いと計算コストがとても大きくなってしまいます。また、学習データが増えるたびに全ての学習データで再学習が必要となってしまいます。

確率的勾配降下法とは

確率的勾配降下法は学習データをシャッフルした上で学習データの中からランダムに1つを取り出して誤差を計算し、パラメーターを更新をします。勾配降下法ほどの精度は無いが増えた分だけの学習データのみで再学習する(重みベクトルの初期値は前回の学習結果を流用)ため再学習の計算量が圧倒的に低くなります。
運が良ければ最急降下法よりも早く最適解にたどり着けますが、運が悪ければいつまで経っても適した答えを導けません。

ミニバッチ確率的勾配降下法とは

ミニバッチ確率的勾配降下法は最急降下法と確率的勾配降下法の間を取ったような形となります。最急降下法では時間がかかりすぎ、確率的勾配降下法では一つ一つのデータにかなり揺さぶられることになるので、学習データの中からランダムにいくつかのデータを取り出して誤差を計算、パラメーターを更新をします。このときの一回に取り出すデータの数をバッチサイズと呼びます。

最急降下法と確率的勾配降下法の違い

パラメーター更新の式

最急降下法のパラメーター更新の式
$\displaystyle \theta_j := \theta_j - \eta\sum_{i=1}^n(f_{\theta}({x}^{(i)}) - y^{(i)}){x_j}^{(i)}$

確率的勾配降下法のパラメーター更新の式
$\displaystyle \theta_j := \theta_j - \eta(f_{\theta} ({x}^{(k)}) - y^{(k)}){x_j}^{(k)}$
(式中のkは、パラメーター更新毎にランダムに選ばれたインデックス)

大きな違いとして、確率的勾配降下法ではシグマ $\sum$ (1～nまで合計)が取れています。
その分、計算コストは少なくなっていることが分かりますよね。

最小値へのたどり着き方

最急降下法がほぼ直線的に最小値にたどり着くのに対し、確率的勾配降下法はランダムなのでくねくねしながら最小値にたどり着きます。
f:id:Yaju3D:20170925010546p:plain

局所解に陥る可能性

誤差関数が素直なカーブのみならいいですが、下図のようにいったん下がってまた上がるみたいなうねうねした場合があります。本当は④が最小値なのに別の小さな谷(これを局所解といいます)に捕まってしまうことがあります。
f:id:Yaju3D:20170917223314p:plain

確率的勾配降下法はこのうねうねのいろいろなところから勾配を下ろうとするため、最急降下法よりも局所解に陥る可能性が小さくなります。

定数η(イータ)は学習係数と呼ばれます。このηは人が移動する際の「歩幅」と見立てられます。このηで決められた値に従って次に移動する点が決められるからです。その歩幅が大きいと最小値に達しても、それを飛び越えてしまう危険があります(下図左)。歩幅が小さいと、極小値で停留してしまう危険があります(下図右)。
f:id:Yaju3D:20170925010945p:plain

最後に

言葉で説明だけだと分かりにくいので、実際にPythonでプログラムされているサイトを見つけました。 sinhrks.hatenablog.com

これを、組み直ししてみました。 qiita.com

次回は、勾配降下法を実際に計算してみます。

参照

2017-07-24

ディープラーニング(深層学習)を理解してみる(勾配降下法)

機械学習 tensorflow 人工知能

はじめに

機械学習をやる上では「勾配降下法」を理解しておきたい。
「勾配降下法」で検索すると自分が書いた記事が見つかります。 yaju3d.hatenablog.jp

資料を元に書いた記事なので当時はよく理解していたわけではないですが、今、読み返すとふむふむと言ったところです。今回はもっと深く追求していきます。

機械学習は最適解を求めるのが目的です。
上記記事の八百屋の件でも、条件が当てはまる最小の値をひたすら繰り返し計算すれば求めることが出来るのですが、これを出来るだけ少ない計算で最小値を見つけるようにしたい。ここで「勾配降下法」を使うことになるわけです。

解けない連立方程式

どうせなので八百屋の問題を使います。

例題 1

リンゴ１個とミカン３個を買うと１９０円、リンゴ３個とミカン１個を買うと３３０円するようです。
リンゴ２個とミカン４個を買うといくらになるでしょうか？ f:id:Yaju3D:20160417225841p:plain

今回は数式で表してみます。次の連立方程式となります。

$\displaystyle \begin{cases} a + 3b &=& 190 \\ 3a + b &=& 330 \\ \end{cases}$

加減法で計算します。

$\displaystyle \begin{eqnarray} 3a + 9b &=& 570 \\ -) 3a + b &=& 330 \\ \\ 8b &=& 240 \\ 　　　　 b &=& 30　 \end{eqnarray}$

$\displaystyle \begin{eqnarray} a + 3b &=& 190 \\ a + 3\times30 &=& 190 \\ a &=& 190-90 \\ a &=& 100 \end{eqnarray}$

$a=100$ と $b=30$ と分かりましたので、値を入れると答えが $320$ と求まります。

f:id:Yaju3D:20160417230109p:plain f:id:Yaju3D:20160417230118p:plain

例題 2

例題 1 に対し、更にリンゴ５個とミカン７個を買うと６６０円を追加した場合
リンゴ２個とミカン４個を買うといくらになるでしょうか？
f:id:Yaju3D:20160417230234p:plain

先程と同様に連立方程式を書いてみます。

$\displaystyle \begin{cases} a + 3b &=& 190 \\ 3a + b &=& 330 \\ 5a + 7b &=& 660 \end{cases}$

先程の答えの $a=100$ と $b=30$ を入れても答えが $100\times5 + 30\times7 = 500 + 210 = 710$ となり答えの $660$ にはなりません。

f:id:Yaju3D:20160417230455p:plain

中学校で勉強する連立方程式は、未知数(パラメータの数)が２個であれば、方程式の数も２本でなければなりません。例題 2は、方程式の数が多すぎるということになります。とは言え、実際の世の中の現象は、このようにデータがバラバラなケースのほうが多いですよね。
そこで出来るだけ近い値である近似値を求めることにするわけです。

近似値を求める

今回、近似値を求めるのには最小2乗法を使います。

最小二乗法とは、モデル関数を $f(x)$ とするとき、

$\displaystyle \sum_{i=1}^n\{y_i-f(x)\}^2$

が最小となるような $f(x)$ を求めることである。 sci-pursuit.com

下図に合わせて、最小二乗法の式を変更してみます。

$x_i$ がリンゴの個数、 $y_i$ がミカンの個数、 $z_i$ が合計値とする。

$a$ がリンゴの価格、 $b$ がミカンの価格の最小値を求める。

$\displaystyle \frac{1}{3}\sum_{i=1}^n\{(ax_i + by_i)-z_i\}^2$

最後に平均しているので３で割っていますが、最小値を求める上で平均ではなく合計したままでも、最小二乗法の公式通りに２で割っても最終的に求まる結果は変わらないです。

f:id:Yaju3D:20160417230639p:plain
条件が当てはまる最小の値をひたすら繰り返し計算する。
f:id:Yaju3D:20160417230656p:plain f:id:Yaju3D:20160417230833p:plain

たくさん計算した結果、最小の値として、 $a=90$ と $b=30$ が求まりました。

少ない計算で最小値を求める

最小二乗法では1回の計算で（一発で）パラメータを求める方式です。データを追加する度に再度計算し直すことになります。少ないデータ量の時はいいですが、データ量が膨大になるとシステムの対応が難しくなってきます。

もし、データを追加するたびにパラメータを更新していく方式ができるなら、変化点だけの少ない計算で最小値を求めることができるようになります。
f:id:Yaju3D:20160417230848p:plain
それが、「勾配降下法」という方法となります。

続きは後日書きます。

2017-06-25

ディープラーニング(深層学習)を理解してみる(TensorFlow Playgroundを試す)

機械学習 tensorflow 人工知能

はじめに

前回はパーセプトロンを多層にすることで、線型分離可能でない問題を解けることを学びました。
yaju3d.hatenablog.jp

これを視覚として見ながら学びたいということで見つけたのが「TensorFlow Playground」となります。
f:id:Yaju3D:20170624220010p:plain

しかし、初見では何がなんだか分からないので「TensorFlow Playground」のことを書いている幾つかのブログを参考に学んでいきます。

TensorFlow Playgroundとは

TensorFlow Playgroundは、A Neural Network Playgroundとも呼ばれ、Daniel SmilkovさんとShan Carterさんが開発したニューラルネットワークの仕組みを理解するための教育コンテンツです。

TensorFlow Playgroundの日本語訳を書いてくれているのが「TensorFlow Playgroundの仕組み」です。

目的

下図のように青とオレンジの正しい区切りの位置を見つけるということです。
直線だと簡単に分離できる問題もあれば、円形という複雑な問題もあるわけです。
f:id:Yaju3D:20170604230608p:plain

使い方

例題 Circle(円)、Gaussian(ガウシアン)、Exclusive or(排他or:XOR)、Spiral(螺旋)
f:id:Yaju3D:20170626230724p:plain

全体レイアウト

f:id:Yaju3D:20170625120546p:plain

①は、DATA(データ)は例題となります。例題は4つあり初期値は円となっています。
②は、FEATURES(特徴)は、入力するデータの特徴となります。特徴は7つあり初期値は上2つとなっています。
③は、HIDDEN LAYERS(隠れ層)は中間層となります。中間層の数を「+」と「-」ボタンで増減でき初期値は2段となっています。
④は、neurons(ニューロン)は、各隠れ層のノードとなります。
※各ノードをマウスオーバーすると⑥で拡大して見れます。ニューロンは重みの影響を受け、重みは線の太さと色で表されます。
- ④-1が先頭の中間層で初期値は4ニューロンとなります。
- ④-2が最後の中間層で初期値は2ニューロンとなります。
⑤は、再生ボタンとなります。決定したモデルを実際に動かします。
⑥は、出力結果となります。
⑦は、Test loss(誤差(テスト))とTraining loss(誤差(トレーニング))の数値となります。

実際に動かしてみよう

デフォルト状態で再生してみます。右側の出力結果の平面上に点在したオレンジと青の点々に沿うようにヒートマップの色が変化していく様子が見れるはずです。そして点々の色とヒートマップの色の分布が互いに近づいてくるに従って誤差の数値が小さくなる様子も確認できるはずです。

青枠⑦のTest loss(誤差(テスト))とTraining loss(誤差(トレーニング))の数値を見ます。これが少ないほど良い結果になります。
Epochが50くらいで図上では分離されていますが、誤差の数値的には0.022とまだあります。
Epochが100くらいで誤差の数値的には0.008くらいまで下がります。
Epochが500くらいまでいくと誤差が0.0001まで下がります。

パラメーターをいじってみる

④-1の先頭の中間層を4ニューロンから3ニューロンに減らしてみます。
f:id:Yaju3D:20170625134326p:plain
これだとあまり変化なく、Epochが500くらいまでいくと誤差が0.0001まで下がります。
さらに2層まで減らすとEpochが1000までいっても収束しません。

今度は、中間層を1つ増やしてみます。
f:id:Yaju3D:20170625145117p:plain
Epochが200くらいまでいくと誤差が0.0001まで下がるので、収束は速くなります。

各パラメーターの説明

TensorFlow Playgroundの日本語訳「TensorFlow Playgroundの仕組み」から一部抜粋します。

上側パラメーター

Epoch(エポック)は、学習させる回数です。用意された全トレーニングデータをニューラルネットワークに投入しパラメータを更新、修正し終えると機械学習の1サイクル(1エポック)が完了します。統計モデルの種類が分類の場合、トレーニングデータは500個なので、この500個全部をトレーニングに使い切ると1エポック完了したことになります。
Learning rate(学習率)は、一度の学習でどの程度重みやバイアスの値を修正するかの率を表します。学習率が大きいと1度に修正される重み、バイアスの量が大きくなります。小さくすると重み、バイアスの値を1度に少しだけ修正しようとします。
Activation(活性化関数)は、ニューロンの出力をフィルタリングします。tanh、ReLU、Sigmoid(シグモイド関数)、Liner(線形関数)があります。
Regularization(正則化)は、過学習を防ぐための仕組みです。None, L1, L2 があります。
Regularization rate(正則化項)は、正則化されたニューラルネットワークに対して正則化項を加えることで、より過学習を防ぐようになります。
Problem type(統計モデルの種類)は、「Classification(分類)」と「Regression(回帰)」の2種類があります。
- Classification(分類)は、入力した画像が猫であるか猫でないかを0/1で判断する。分類の図は点々がブルー(+1)かオレンジ(-1)かの二通りの出力結果のデータの分布となります。
- Regression(回帰)は、得点の値について-1,1だけのとびとびの離散的な値だけでなく、その間の-0.529や0.29039などの-1から+1までの連続的な中間値も考慮に入れます。入力した画像が猫である確率を求める場合に使います。回帰の図は分類と同様に点々がブルー(+1)かオレンジ(-1)であることには変わりありませんが、白味がかった-1と+1の間の中間の値のデータも含まれます。

左側パラメーター

Ratio of training to test data(トレーニングデータの割合)は、「Classification(分類)」が500個、「Regression(回帰)」が1200個のデータのサンプル数となっていますので、例えばトレーニングデータの割合を60%とすると、500個のデータサンプルの内300個をトレーニングデータに、 200個のデータをテストデータに回します。
Noise(ノイズ)は、円やガウシアンなどの選択したデータセットに対してかけるノイズ(0〜50まで5刻みで設定)で数値は%単位です。
Batch size(バッチサイズ)は、1回の学習(重み、バイアスの更新)を何個のトレーニングデータで実施するかを決める数値です。例えば1エポックで500回学習とした場合にバッチサイズが25にすると、1エポックで20回学習することになります。
REGENARATE(再生成)は、データを再生成します。

右側下パラメーター

f:id:Yaju3D:20170626231602p:plain

Show test data(テストデータを表示する)は、チェックボックスをオンにするとテストデータが表示されます。テストデータはニューラルネットワークに教えるためには使わないデータで、このデータを使ってニューラルネットワークが正しく学習できたかを検証します。
Discretize output(出力を離散化する)は、チェックボックスをオンにすると答えが曖昧でも、最終的にどちらの答えになるのかをハッキリさせることが出来ます。

過学習

過学習が発生すると、十分に小さなTraining loss(誤差(トレーニング))に対して、Test loss(誤差(テスト))が小さくならない現象が発生します。TensorFlow Playgroundで意図的に過学習を起こすことは簡単です。画面左側の「Ratio of training to test data(トレーニングデータの割合)」を10%まで下げてみます。
f:id:Yaju3D:20170626234708p:plain

スライド

Playgroundでディープラーニングを勉強しよう from Hiroyuki Yoshida

例題

Problem type(統計モデルの種類)の「Classification(分類)」だけ他の例題を自分なりにやってみました。
これが正しいわけでもなく、再更新すると違う結果になったりすることもあります。

Gaussian(ガウシアン)

一番単純です。Activation(活性化関数)をLiner(線形関数)にしています。
f:id:Yaju3D:20170626232335p:plain

Exclusive or(排他or:XOR)

XORは線形分離不可能な問題です。特徴量にX1X2があるのでそのまま使っています。
f:id:Yaju3D:20170626233038p:plain

別方法として特徴量は先頭2つでやってみました。Activation(活性化関数)をReLUにすると直角的になります。
f:id:Yaju3D:20170627215236p:plain

Spiral(螺旋)

特徴量を全て使っています。過学習を防ぐためRegularization(正則化)をL1、Regularization rate(正則化項)を0.001にしてます。
なかなかTest loss(誤差(テスト))が下がらなくて、0.008が限界でした。
f:id:Yaju3D:20170626233502p:plain

特徴量を減らして、中間層を増やしてみました。Test loss(誤差(テスト))は、0.006になりました。
f:id:Yaju3D:20170627234331p:plain

はじめに

人工知能による予測化を断念

次の手の予測アルゴリズム

2017年の勝敗結果

スライド

最後に

はじめに

プログラム

重みの更新

はじめに

勾配降下法

１.初期設定

２．変位ベクトルを算出

各計算結果の求め方

３．位置を更新

４．２と３の繰り返し

バイアスについて

切片(せっぺん)

閾値(しきいち)

バイアスの式表現

リンゴとミカン

前提

勾配の計算式

初期値の設定

重みの更新

①現在の重みで推測値を求める

②勾配を計算する

③重みを更新する

更新の繰り返し

最後に

はじめに

ベクトル

内積の計算

参照

最小値

勾配降下法に適用

参照

はじめに

勾配降下法

最急降下法とは

確率的勾配降下法とは

ミニバッチ確率的勾配降下法とは

最急降下法と確率的勾配降下法の違い

パラメーター更新の式

最小値へのたどり着き方

局所解に陥る可能性

最後に

参照

はじめに

解けない連立方程式

例題 1

例題 2

近似値を求める

少ない計算で最小値を求める

はじめに

TensorFlow Playgroundとは

目的

使い方

全体レイアウト

実際に動かしてみよう

パラメーターをいじってみる

各パラメーターの説明

上側パラメーター

左側パラメーター

右側下パラメーター

スライド

例題

Gaussian(ガウシアン)

Exclusive or(排他or:XOR)

Spiral(螺旋)

参照

勾配 $\Delta E$ の計算式

②勾配 $\Delta E$ を計算する